WordNet
- X-ray machine in which a computer builds a detailed image of a particular plane through an object from multiple X-ray measurements
Wikipedia preview
出典(authority):フリー百科事典『ウィキペディア(Wikipedia)』「2013/09/02 12:42:29」(JST)
wiki ja
UpToDate Contents
全文を閲覧するには購読必要です。 To read the full text you will need to subscribe.
- 1. 胸部CTの原理 principles of computed tomography of the chest
- 2. 肺の高分解能CT high resolution computed tomography of the lungs
- 3. 造影剤誘発性腎症の病因、臨床的特徴、および診断 pathogenesis clinical features and diagnosis of contrast induced nephropathy
- 4. 成人におけるてんかんの外科的治療 surgical treatment of epilepsy in adults
- 5. 成人における確定診断を得られていない低血圧やショックの評価および初期アプローチ evaluation of and initial approach to the adult patient with undifferentiated hypotension and shock
Japanese Journal
- タウイメージングの開発 (認知症医療の新展開 : アルツハイマー病研究会 記録) -- (トラックセッション 診断学 : タウ関連を中心に,最新知識の提供)
- 樋口 真人,丸山 将浩,島田 斉 [他]
- 老年精神医学雑誌 25 (312増刊1), 69-75, 2014-03
- NAID 40020026550
- Molecular imagingによる冠動脈プラーク評価 (第1土曜特集 循環器と画像診断Update) -- (非侵襲的画像診断Update)
- 吉永 恵一郎,玉木 長良
- 医学のあゆみ 248(5), 398-402, 2014-02-01
- NAID 40019962821
- ガンマ線医用イメージング : 陽電子断層撮影法(PET)機器開発研究の最新動向 (小特集 ガンマ線イメージングの最新動向)
- 山谷 泰賀
- Journal of the Vacuum Society of Japan = 真空 57(2), 45-50, 2014-02
- NAID 40019974870
Related Links
- 世界大百科事典 第2版 断層撮影の用語解説 - X線検査における一手法。普通のX線撮影では種々の構造が重積して1枚の画像を形成するが,断層撮影は,目的とする身体のある深さの断面のみを明りょうなX線像として写し出し,他 ...
- 肺がんの診断のために実施される検査方法をご紹介しています。(断層撮影) ... 「ある物体の全体をそのまま投影した影絵の形で見るよりも、その物体を輪切り、あるいは薄切りにした方が内部が良くわかるのではないか。
Related Pictures
★リンクテーブル★
| 国試過去問 | 「106F029」「106A023」「106D023」「089A088」 |
| リンク元 | 「tomograph」「断層撮影法」「プラニグラフィ」「断層撮影機」 |
| 拡張検索 | 「エックス線断層撮影」「陽電子放射断層撮影法」「断層撮影像」「コンピューター断層撮影」「コンピュータ体軸断層撮影」 |
| 関連記事 | 「撮影」「断層」「影」 |
「106F029」
- 次の文を読み、 28、 29の問いに答えよ。
- 67歳の男性。全身の衰弱を心配した家族に伴われて来院した。
- 現病歴: 3か月前から徐々に体重が減少し、 2か月前から外出できなくなり、 1週前からは家族の介助がないと立ち上がれなくなった。患者本人は受診を嫌がっていたが、 2日前からはほとんど食事が摂れず、トイレまで歩くこともできなくなったため受診に同意した。
- 既往歴:健康診断は受けていない。
- 生活歴:喫煙は60本/日を47年間。飲酒は日本酒1-2合/日を47年間。
- 家族歴 :父親が高血圧症で、脳梗塞のため82歳で死亡。
- 現 症:意識は清明。身長165cm、体重42kg。体温37.6℃。脈拍120/分、整。血圧96/62mmHg。呼吸数16/分。 SpO2 95%(room air)。眼瞼結膜に貧血を認めない。頸静脈の怒張を認めない。右の前胸部、背部および側胸部で呼吸音が減弱している。 coarse cracklesを聴取しない。皮膚のツルゴールが低下している。下腿に浮腫を認めない。
- 検査所見:血液所見:赤血球394万、 Hb13.1g/dL、 Ht40%、白血球11,700(好中球85%、好酸球1%、単球6%、リンパ球8%)、血小板50万。血液生化学所見:随時血糖181mg/dL、 HbA1c6.5%(基準4.3-5.8)、総蛋白7.3g/dL、アルブミン2.3g/dL、尿素窒素28mg/dL、クレアチニン0.6mg/dL、尿酸3.8mg/dL、総ビリルビン0.3mg/dL、 AST47IU/L、 ALT28IU/L、LD391IU/L(基準176-353)、ALP435IU/L(基準115-359)、 γ-GTP44IU/L(基準8-50)、 Na133mEq/L、 K5.0mEq/L、 Cl93mEq/L、 Ca9.6mg/dL。 CRP24mg/dL。胸部エックス線写真(別冊No. 4)を別に示す。
- 次に行うべき検査はどれか。
※国試ナビ4※ [106F028]←[国試_106]→[106F030]
「106A023」
- 65歳の男性。頚部腫瘤を主訴に来院した。 6か月前から頚部に腫瘤を自覚しており、徐々に増大してきたため受診した。眼瞼結膜に貧血を認めない。左頚部に径2cmのリンパ節を3個、右腋窩に径2cmのリンパ節を1個触知する。いずれも弾性硬で圧痛はない。心音と呼吸音とに異常を認めない。腹部は平坦、軟で、肝・脾を触知しない。血液所見:赤血球398万、 Hb11.0g/dl、 Ht38%、白血球6,300、血小板23万。血液生化学所見:総蛋白7.5g/dl、アルブミン4.8g/dl、尿素窒素19mg/dl、クレアチニン0.9mg/dl、総ビリルビン0.8mg/dl、 AST31IU/l、 ALT28IU/l、 LD447IU/l(基準176-353)。胸腹部造影CTで縦隔リンパ節、腹腔内リンパ節および脾臓の腫大を認める。
- 次に行う検査として最も適切なのはどれか。
※国試ナビ4※ [106A022]←[国試_106]→[106A024]
「106D023」
- 60歳の女性。健康診断の胸部エックス線写真で異常を指摘され来院した。自覚症状はない。既往歴に特記すべきことはない。喫煙歴はない。身長153cm、体重55kg。体温36.8℃。脈拍60/分、整。血圧118/64mmHg。呼吸数16/分。 SpO2 99%(room air)。心音と呼吸音とに異常を認めない。血液所見:赤血球380万、Hb13.2g/dl、 Ht33%、白血球5,600、血小板23万。 CRP 0.3mg/dl。胸部エックス線写真(別冊No. 7A)と胸部単純CT(別冊No. 7B)とを別に示す。
- 診断のために行うべき検査として最も有用なのはどれか。
※国試ナビ4※ [106D022]←[国試_106]→[106D024]
「089A088」
- 排泄性胆道造影法で正しいのはどれ
「tomograph」
「断層撮影法」
「プラニグラフィ」
- 英
- planigraphy
- 関
- 断層撮影
![{l}_{[\theta,s]}(t) =\begin{bmatrix}
s\cos \theta -t\sin \theta \\
s\sin \theta + t\cos \theta \\
\end{bmatrix}](http://upload.wikimedia.org/math/5/e/8/5e868b66d488199b79a5ade607c675fb.png)

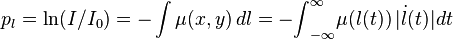



![{l}_{[\theta,s]}(t) =t
\begin{bmatrix}
-\sin \theta \\
\cos \theta \\
\end{bmatrix} +
\begin{bmatrix}
s\cos \theta \\
s\sin \theta \\
\end{bmatrix}](http://upload.wikimedia.org/math/a/b/6/ab6af33af016e8d11449b7c0d4f9ca7f.png)

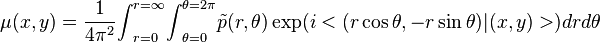
 の証明
の証明

















