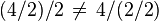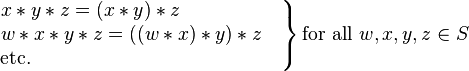- adj.
- 連合性の、連合の
WordNet
- characterized by or causing or resulting from the process of bringing ideas or events together in memory or imagination ; "associative learning" (同)associatory
- united or combined; "a joint session of Congress"; "joint owners"
- marijuana leaves rolled into a cigarette for smoking (同)marijuana cigarette, reefer, stick, spliff
- a disreputable place of entertainment
- junction by which parts or objects are joined together
- (anatomy) the point of connection between two bones or elements of a skeleton (especially if it allows motion) (同)articulation, articulatio
- provide with a joint; "the carpenter jointed two pieces of wood" (同)articulate
- affecting or involving two or more; "joint income-tax return"; "joint ownership"
- fasten with a joint
- fit as if by joints; "The boards fit neatly"
- involving both houses of a legislature; "a joint session of Congress"
- separate (meat) at the joint
- the act of consorting with or joining with others; "you cannot be convicted of criminal guilt by association"
- (chemistry) any process of combination (especially in solution) that depends on relatively weak chemical bonding
- a relation resulting from interaction or dependence; "flints were found in association with the prehistoric remains of the bear"; "the host is not always injured by association with a parasite"
- the state of being connected together as in memory or imagination; "his association of his father with being beaten was too strong to break"
- the process of bringing ideas or events together in memory or imagination; "conditioning is a form of learning by association" (同)connection, connexion
- (ecology) a group of organisms (plants and animals) that live together in a certain geographical region and constitute a community with a few dominant species
- a formal organization of people or groups of people; "he joined the Modern Language Association"
- of trade unions; "the union movement"; "union negotiations"; "a union-shop clause in the contract"
- healing process involving the growing together of the edges of a wound or the growing together of broken bones (同)conglutination
- the state of being joined or united or linked; "there is strength in union" (同)unification
- the act of making or becoming a single unit; "the union of opposing factions"; "he looked forward to the unification of his family for the holidays" (同)unification, uniting, conjugation, jointure
- a device on a national flag emblematic of the union of two or more sovereignties (typically in the upper inner corner)
- an organization of employees formed to bargain with the employer; "you have to join the union in order to get a job" (同)labor_union, trade union, trades union, brotherhood
- a set containing all and only the members of two or more given sets; "let C be the union of the sets A and B" (同)sum, join
- a political unit formed from previously independent people or organizations; "the Soviet Union"
- the occurrence of a uniting of separate parts; "lightning produced an unusual union of the metals"
- having partial rights and privileges or subordinate status; "an associate member"; "an associate professor"
- a person who joins with others in some activity or endeavor; "he had to consult his associate before continuing"
- a person with subordinate membership in a society, institution, or commercial enterprise; "associates in the law firm bill at a lower rate than do partners"
- any event that usually accompanies or is closely connected with another; "first was the lightning and then its thunderous associate"
- make a logical or causal connection; "I cannot connect these two pieces of evidence in my mind"; "colligate these facts"; "I cannot relate these events at all" (同)tie_in, relate, link, colligate, link up, connect
- the act of constituting a political unity out of a number of separate states or colonies or provinces so that each member retains the management of its internal affairs
- an organization formed by merging several groups or parties
- of or relating to associations or associationism
- not associative
PrepTutorEJDIC
- 連合の;連想の
- 『関節』 / 『継ぎ目』,接合箇所,合わせ目 / 継ぎ目と継ぎ目の間の部分,節 / (二つの部分を継いだり支えたりするのに用いる)継ぎ手,ジョイント / (枝や葉の)つけ根,節 / (骨付きの)肉の大切り身 / 《俗》安酒場,とばく宿,アヘン窟(くつ) / 『共同の』,共有の;連帯の,連合の / 両院合同の;二院制議会の両院の / …‘を'継ぎ合わせる;…‘を'継ぎ目(関節)でつなぐ / …‘を'継ぎ目で分ける;〈鳥・肉など〉‘を'関節で切り分ける
- 〈U〉(…との)『交際』,付き合い《+『with』+『名』》 / 〈U〉(…との)『連合』,『共同』,関連《+『with』+『名』》 / 〈C〉組合,協会,会社 / 〈U〉連想;〈C〉《しばしば複数形で》連想されるもの
- 〈U〉(…の,の間の)『結合』,合同,合併;調和,一致《+of(between)+名》 / 〈C〉『結合したもの』,結合体,統一組識 / 《the U-》アメリカ合衆国;(南北戦争時に)連邦政府側についた北部諸州 / 《the U-》英連合王国(1706年イングランドとスコットランドが合併) / 〈C〉『労働組合』同盟,ユニオン / 〈C〉〈U〉結婚[生活] / 〈C〉連合旗章(米国国旗の白星;英国国旗の3本十字の三国連合旗章など) / 〈C〉(機械の部品をくなぐ)接合管
- 〈人〉'を'(…の)『仲間に加える』,(…に)連合させる《+『名』〈人〉+『with』+『名』》 / (…と)…'を'結びつけて考える(起こす)《+『名』+『with』+『名』》 / (…と)『仲間になる』,交際する《+『with』+『名』》 / (…と)合体する,提携する《+『with』+『名』》 / 『仲間』,『同僚』;組合員 / 準会員 / 付属物;連想されるもの / 連合した;仲間の,同僚の / 補助の,準…
- 〈C〉連合,連盟 / 〈C〉連邦制度;連邦政府 / 〈U〉連邦にすること
Wikipedia preview
出典(authority):フリー百科事典『ウィキペディア(Wikipedia)』「2015/10/15 13:57:35」(JST)
wiki en
UpToDate Contents
全文を閲覧するには購読必要です。 To read the full text you will need to subscribe.
- 1. 離人・現実感喪失障害:疫学、病因、臨床症状、経過および診断 depersonalization derealization disorder epidemiology pathogenesis clinical manifestations course and diagnosis
- 2. 大麻の使用と障害:疫学、併存症、健康に及ぼす影響、法医学的な位置付け cannabis use and disorder epidemiology comorbidity health consequences and medico legal status
- 3. 新生児における脳室内出血のマネージメントおよび合併症 management and complications of intraventricular hemorrhage in the newborn
- 4. クライネ・レビン症候群(反復性過眠症) kleine levin syndrome recurrent hypersomnia
- 5. 後方循環系の脳血管症候群 posterior circulation cerebrovascular syndromes
English Journal
- Inhibition of PKMζ in the nucleus accumbens core blocks the expression of locomotor sensitization induced by amphetamine.
- Song MJ, Jang JK, Kim WY, Yoon HS, Kim JH.SourceDepartment of Physiology, Brain Korea 21 Project for Medical Science, Brain Research Institute, Yonsei University College of Medicine, Seoul 120-752, South Korea.
- Behavioural brain research.Behav Brain Res.2013 Mar 15;241:139-43. doi: 10.1016/j.bbr.2012.12.007. Epub 2012 Dec 12.
- Behavioral sensitization is a form of drug-induced, long-lasting, non-associative memory. Protein kinase M zeta (PKMζ) has been shown to play a role in maintaining associative long-term memory in various brain regions. In the present study, rats were pre-exposed to either saline or amphetamine (AMP
- PMID 23246525
- Asymmetric hemispheric contribution to ERPs in associative memory indexes goal relevance and quantity of information.
- Pergola G, Trotta M, Suchan B.SourceCognitive Neuroscience Sector, International School for Advanced Studies (SISSA-ISAS), via Bonomea 265, I-34136 Trieste, Italy; Department of Neuropsychology, Institute of Cognitive Neuroscience, Ruhr-University Bochum, D-44780 Bochum, Germany; International Graduate School of Neuroscience, Ruhr-University Bochum, D-44780 Bochum, Germany. Electronic address: giuliopergola@yahoo.it.
- Behavioural brain research.Behav Brain Res.2013 Mar 15;241:7-16. doi: 10.1016/j.bbr.2012.11.041. Epub 2012 Dec 5.
- Explicit encoding requires humans to select the information relevant to their goals, yet not all irrelevant information is discarded. The present study addressed how different quantity and relevance of information modulate the electrophysiological activity during the encoding and retrieval phases of
- PMID 23220030
- Contingent choice. Exploring the relationship between sweetened beverages and vegetable consumption.
- Cornwell TB, McAlister AR.SourceLundquist College of Business, 1208 University of Oregon, University of Oregon, Eugene, OR 97403-1208, USA. Electronic address: tbc@uoregon.edu.
- Appetite.Appetite.2013 Mar;62:203-8. doi: 10.1016/j.appet.2012.05.001. Epub 2012 May 14.
- Adults and children are repeatedly exposed to the pairing of food and drink as found in meal deals and "combos". There may arise from this indoctrination, a contingent relationship between drink context and food preference. Our multi-method research examines food and drink combining. A survey-based
- PMID 22595286
- Affective value and associative processing share a cortical substrate.
- Shenhav A, Barrett LF, Bar M.SourceDepartment of Psychology, Harvard University, Cambridge, MA, 02138, USA, ashenhav@princeton.edu.
- Cognitive, affective & behavioral neuroscience.Cogn Affect Behav Neurosci.2013 Mar;13(1):46-59. doi: 10.3758/s13415-012-0128-4.
- The brain stores information in an associative manner so that contextually related entities are connected in memory. Such associative representations mediate the brain's ability to generate predictions about which other objects and events to expect in a given context. Likewise, the brain encodes and
- PMID 23090717
Japanese Journal
- ニューロンCMOSインバータを用いた最小ハミング距離検索連想メモリ (特集 電子回路関連技術)
- 電気学会論文誌. C, 電子・情報・システム部門誌 = IEEJ transactions on electronics, information and systems 136(1), 36-42, 2016-01
- NAID 40020703259
- A SOI Cache-Tag Memory with Dual-Rail Wordline Scheme
- IEICE Transactions on Electronics E99.C(2), 316-330, 2016
- NAID 130005121974
- Study on the Protection of the Lama Temple Heritage in Inner Mongolia as a Cultural Landscape
- Journal of Asian Architecture and Building Engineering 15(1), 9-16, 2016
- NAID 130005119881
- ニューロンCMOSインバータを用いた最小ハミング距離検索連想メモリ
- 電気学会論文誌. C 136(1), 36-42, 2016
- NAID 130005116468
Related Links
- (ə-sō'shə-tĭv) Of or relating to the property of an operation, such as addition or multiplication, which states that the grouping of numbers undergoing the operation does not change the result. For example, 3 + (4 + 5) is equal to (3 ...
- associativeとは。意味や和訳。[形]共同[結合,連想]の;結合[連想]しやすいan associative responsibility連帯責任.as・so・ci・a・tive・ly[副] as・so・ci・a・tive・ness[名] - goo英和辞書は14万項目以上を収録し、発音、音声、慣用句 ...
- Definition of ASSOCIATIVE 1: of or relating to association especially of ideas or images 2: dependent on or acquired by association or learning 3: of, having, or being the property of combining to the same mathematical result ...
Related Pictures
★リンクテーブル★
| リンク元 | 「associate」「union」「連合性」「federation」「associational」 |
| 拡張検索 | 「associative memory」「associative strength」 |
「associate」
- vt.
- 結合する、連合させる。連想によって結びつける。(人を)仲間/友達などとしての関係に置く。(化)会合させる
- vi.
- 仲間/友人などとして交際する(with)。一つにまとめる、連合する
- n.
- 仕事仲間、提携者、同僚。友人、朋友。準会員。従業員、社員
- 密接な蒸す偽付きのある物、付随する物、つきもの。準国家
- 連想によって心に浮かぶ言葉/思い、連想物
- adj.
- 仲間の、同僚の。製紙機械員に次ぐ資格の
- 付随する、連想される
- 関
- accompany、association、associative、attach、bearing、bind、binding、bond、bonding、coassemble、colleague、combine、conjoin、conjugate、conjugation、conjunction、connect、connection、correlate、correlation、couple、dock、engage、engagement、federation、implication、join、joint、ligate、link、linkage、peer、pertinent、reference、relate、relation、relationship、relative、relevance、relevant、symphysial、union
「union」
- n.
- 関
- associate、association、associative、bind、binding、bond、bonding、coalesce、coalescence、coalescent、combine、conjoin、conjugate、conjugation、conjunction、connect、connection、couple、dock、engage、engagement、federation、fusion、join、joint、ligate、linkage、symphysial、symphysis
「連合性」
- 英
- association、associative、associational
- 関
- 会合、関連、共生、対合、連関、連合、群集、協会
「federation」
- n.
「associational」
- 連合性の
「associative memory」
「associative strength」
- 関
- avidity