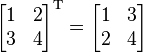v.

転位する、置き換える、転置する

関: dislocation、displacement、ectopia、migrate、migration、migratory、rearrangement、translocation、transposition、transpositional

WordNet

transfer a quantity from one side of an equation to the other side reversing its sign, in order to maintain equality
change key; "Can you transpose this fugue into G major?"
a matrix formed by interchanging the rows and columns of a given matrix
put (a piece of music) into another key
any abnormal position of the organs of the body (同)heterotaxy
the act of reversing the order or place of (同)reversal
(electricity) a rearrangement of the relative positions of power lines in order to minimize the effects of mutual capacitance and inductance; "he wrote a textbook on the electrical effects of transposition"
(mathematics) the transfer of a quantity from one side of an equation to the other along with a change of sign
(music) playing in a different key from the key intended; moving the pitch of a piece of music upwards or downwards
(genetics) a kind of mutation in which a chromosomal segment is transfered to a new position on the same or another chromosome
a displacement of a part (especially a bone) from its normal position (as in the shoulder or the vertebral column)
the act of disrupting an established order so it fails to continue; "the social dislocations resulting from government policies"; "his warning came after the breakdown of talks in London" (同)breakdown
an event that results in a displacement or discontinuity (同)disruption
(genetics) an exchange of chromosome parts; "translocations can result in serious congenital disorders"
the transport of dissolved material within a plant
the movement of persons from one country or locality to another
(chemistry) the nonrandom movement of an atom or radical from one place to another within a molecule
a group of people migrating together (especially in some given time period)
the periodic passage of groups of animals (especially birds or fishes) from one region to another for feeding or breeding
move periodically or seasonally; "birds migrate in the Winter"; "The workers migrate to where the crops need harvesting"
move from one country or region to another and settle there; "Many Germans migrated to South America in the mid-19th century"; "This tribe transmigrated many times over the centuries" (同)transmigrate
(chemistry) a reaction in which an elementary substance displaces and sets free a constituent element from a compound (同)displacement reaction
(psychiatry) a defense mechanism that transfers affect or reaction from the original object to some more acceptable one
to move something from its natural environment (同)deracination
act of removing from office or employment
changing an arrangement
used of animals that move seasonally; "migratory birds"

PrepTutorEJDIC

〈位置・順序など〉‘を'逆にする,置き換える,移す / (楽曲で)…‘を'移調する / (等式で)…‘を'移項する
置き換え,転位 / (数学で)移項 / (音楽で)移調
位置を変えること / 脱臼(だっきゅう) / 混乱
〈U〉〈C〉移住,(動物の)移動 / 〈C〉《集合的に》(人・動物などの)移動の群
(…から…へ)移住する《+『from』+『名』+『to』+『名』》 / (季節に応じ定期的に)〈鳥・動物が〉移動する,渡る
とって代わること,置き換え / 解職,罷免 / 排水量
再整理,再配列
(定期的に)移動する,移住する / 転々とする,放浪性の

Wikipedia preview

出典(authority):フリー百科事典『ウィキペディア（Wikipedia）』「2015/11/20 00:22:24」(JST)

wiki en

[Wiki en表示]

This article is about the transpose of a matrix. For other uses, see Transposition

Note that this article assumes that matrices are taken over a commutative ring. These results may not hold in the non-commutative case.

The transpose A^T of a matrix A can be obtained by reflecting the elements along its main diagonal. Repeating the process on the transposed matrix returns the elements to their original position.

In linear algebra, the transpose of a matrix A is another matrix A^T (also written A′, A^tr, ^tA or A^t) created by any one of the following equivalent actions:

reflect A over its main diagonal (which runs from top-left to bottom-right) to obtain A^T
write the rows of A as the columns of A^T
write the columns of A as the rows of A^T

Formally, the i th row, j th column element of A^T is the j th row, i th column element of A:

If A is an m × n matrix then A^T is an n × m matrix.

The transpose of a matrix was introduced in 1858 by the British mathematician Arthur Cayley.^[1]

Examples

$\begin{bmatrix} 1 & 2 \end{bmatrix}^{\mathrm{T}} = \, \begin{bmatrix} 1 \\ 2 \end{bmatrix}$

$\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}^{\mathrm{T}} = \begin{bmatrix} 1 & 3 \\ 2 & 4 \end{bmatrix}$

$\begin{bmatrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \end{bmatrix}^{\mathrm{T}} = \begin{bmatrix} 1 & 3 & 5\\ 2 & 4 & 6 \end{bmatrix}$

Properties

For matrices A, B and scalar c we have the following properties of transpose:

The operation of taking the transpose is an involution (self-inverse).
The transpose respects addition.
Note that the order of the factors reverses. From this one can deduce that a square matrix A is invertible if and only if A^T is invertible, and in this case we have (A⁻¹)^T = (A^T)⁻¹. By induction this result extends to the general case of multiple matrices, where we find that (A₁A₂...A_k−1A_k)^T = A_k^TA_k−1^T...A₂^TA₁^T.
The transpose of a scalar is the same scalar. Together with (2), this states that the transpose is a linear map from the space of m × n matrices to the space of all n × m matrices.
The determinant of a square matrix is the same as that of its transpose.
The dot product of two column vectors a and b can be computed as the single entry of the matrix product

which is written as a_i bⁱ in Einstein summation convention.
If A has only real entries, then A^TA is a positive-semidefinite matrix.
The transpose of an invertible matrix is also invertible, and its inverse is the transpose of the inverse of the original matrix. The notation A^−T is sometimes used to represent either of these equivalent expressions.
If A is a square matrix, then its eigenvalues are equal to the eigenvalues of its transpose since they share the same characteristic polynomial.
is a symmetric matrix.^[2]

Special transpose matrices

A square matrix whose transpose is equal to itself is called a symmetric matrix; that is, A is symmetric if

A square matrix whose transpose is equal to its negative is called a skew-symmetric matrix; that is, A is skew-symmetric if

A square complex matrix whose transpose is equal to the matrix with every entry replaced by its complex conjugate (denoted here with an overline) is called a Hermitian matrix (equivalent to the matrix being equal to its conjugate transpose); that is, A is Hermitian if

A square complex matrix whose transpose is equal to the negation of its complex conjugate is called a skew-Hermitian matrix; that is, A is skew-Hermitian if

A square matrix whose transpose is equal to its inverse is called an orthogonal matrix; that is, A is orthogonal if

Transpose of a linear map

The transpose may be defined in a more generally:

If f : V → W is a linear map between right R-modules V and W with respective dual modules V^∗ and W^∗, the transpose of f is the linear map

Equivalently, the transpose ^tf is defined by the relation

where ⟨·,·⟩ is the duality pairing. This definition also applies unchanged to left modules and to vector spaces.^[3]

The definition of the transpose may be seen to be independent of any bilinear form on the vector spaces, unlike the adjoint (below).

If the matrix A describes a linear map with respect to bases of V and W, then the matrix A^T describes the transpose of that linear map with respect to the dual bases.

Transpose of a bilinear form

Every linear map to the dual space f : V → V^∗ defines a bilinear form B : V × V → F, with the relation B(v, w) = f(v)(w). By defining the transpose of this bilinear form as the bilinear form ^tB defined by the transpose ^tf : V^∗∗ → V^∗ i.e. ^tB(w, v) = ^tf(w)(v), we find that B(v, w) = ^tB(w, v).

Adjoint

If the vector spaces V and W have respective nondegenerate bilinear forms B_V and B_W, a concept closely related to the transpose – the adjoint – may be defined:

If f : V → W is a linear map between vector spaces V and W, we define g as the adjoint of f if g : W → V satisfies

These bilinear forms define an isomorphism between V and V^∗, and between W and W^∗, resulting in an isomorphism between the transpose and adjoint of f. The matrix of the adjoint of a map is the transposed matrix only if the bases are orthonormal with respect to their bilinear forms. In this context, many authors use the term transpose to refer to the adjoint as defined here.

The adjoint allows us to consider whether g : W → V is equal to f⁻¹ : W → V. In particular, this allows the orthogonal group over a vector space V with a quadratic form to be defined without reference to matrices (nor the components thereof) as the set of all linear maps V → V for which the adjoint equals the inverse.

Over a complex vector space, one often works with sesquilinear forms (conjugate-linear in one argument) instead of bilinear forms. The Hermitian adjoint of a map between such spaces is defined similarly, and the matrix of the Hermitian adjoint is given by the conjugate transpose matrix if the bases are orthonormal.

Implementation of matrix transposition on computers

On a computer, one can often avoid explicitly transposing a matrix in memory by simply accessing the same data in a different order. For example, software libraries for linear algebra, such as BLAS, typically provide options to specify that certain matrices are to be interpreted in transposed order to avoid the necessity of data movement.

However, there remain a number of circumstances in which it is necessary or desirable to physically reorder a matrix in memory to its transposed ordering. For example, with a matrix stored in row-major order, the rows of the matrix are contiguous in memory and the columns are discontiguous. If repeated operations need to be performed on the columns, for example in a fast Fourier transform algorithm, transposing the matrix in memory (to make the columns contiguous) may improve performance by increasing memory locality.

Ideally, one might hope to transpose a matrix with minimal additional storage. This leads to the problem of transposing an n × m matrix in-place, with O(1) additional storage or at most storage much less than mn. For n ≠ m, this involves a complicated permutation of the data elements that is non-trivial to implement in-place. Therefore efficient in-place matrix transposition has been the subject of numerous research publications in computer science, starting in the late 1950s, and several algorithms have been developed.

References

^ Arthur Cayley (1858) "A memoir on the theory of matrices," Philosophical Transactions of the Royal Society of London, 148 : 17-37. The transpose (or "transposition") is defined on page 31.
^ "Is a matrix multiplied with its transpose something special?" Proof in answer on StackExchange.com,
^ Bourbaki, "II §2.5", Algebra I

External links

MIT Linear Algebra Lecture on Matrix Transposes
Transpose, mathworld.wolfram.com
Transpose, planetmath.org
Khan Academy introduction to matrix transposes

UpToDate Contents

全文を閲覧するには購読必要です。 To read the full text you will need to subscribe.

1. 直腸腟瘻、肛門腟瘻、および結腸膀胱瘻 rectovaginal anovaginal and colovesical fistulas
2. Z形成術 z plasty
3. 血液透析用の動静脈痩形成 creating an arteriovenous fistula for hemodialysis

English Journal

Lipid-protein interactions: Lessons learned from stress.

Battle AR1, Ridone P2, Bavi N3, Nakayama Y2, Nikolaev YA4, Martinac B5.
Biochimica et biophysica acta.Biochim Biophys Acta.2015 Sep;1848(9):1744-56. doi: 10.1016/j.bbamem.2015.04.012. Epub 2015 Apr 25.
Biological membranes are essential for normal function and regulation of cells, forming a physical barrier between extracellular and intracellular space and cellular compartments. These physical barriers are subject to mechanical stresses. As a consequence, nature has developed proteins that are abl
PMID 25922225

Focus on the legislative approach to short half life radioactive hospital waste releasing.

Petrucci C1, Traino AC2.
Physica medica : PM : an international journal devoted to the applications of physics to medicine and biology : official journal of the Italian Association of Biomedical Physics (AIFB).Phys Med.2015 Jun 19. pii: S1120-1797(15)00141-6. doi: 10.1016/j.ejmp.2015.06.001. [Epub ahead of print]
PURPOSE: We propose to summarize the advancements introduced by the new Directive 2013/59/Euratom concerning the concept of clearance, for which the radioactive medical waste represents a typical candidate. We also intend to spotlight disputable points in the regulatory scheme in force in Italy, as
PMID 26099431

Benzothiadiazole Derivatives as Fluorescence Imaging Probes: Beyond Classical Scaffolds.

Neto BA1, Carvalho PH1, Correa JR1.
Accounts of chemical research.Acc Chem Res.2015 Jun 16;48(6):1560-9. doi: 10.1021/ar500468p. Epub 2015 May 15.
This Account describes the origins, features, importance, and trends of the use of fluorescent small-molecule 2,1,3-benzothiadiazole (BTD) derivatives as a new class of bioprobes applied to bioimaging analyses of several (live and fixed) cell types. BTDs have been successfully used as probes for a p
PMID 25978615

The application of the European heat wave of 2003 to Korean cities to analyze impacts on heat-related mortality.

Greene JS1, Kalkstein LS2, Kim KR3, Choi YJ3, Lee DG3.
International journal of biometeorology.Int J Biometeorol.2015 Jun 16. [Epub ahead of print]
The goal of this research is to transpose the unprecedented 2003 European excessive heat event to six Korean cities and to develop meteorological analogs for each. Since this heat episode is not a model but an actual event, we can use a plausible analog to assess the risk of increasing heat on these
PMID 26076864

Japanese Journal

Moe版一般化積型反復法の並列性能評価

藤野清次,岩里洸介,MoeThuThu
情報処理学会研究報告. [ハイパフォーマンスコンピューティング] 2014-HPC-143(20), 1-6, 2014-02-24
本論文では,分散並列環境下での反復解法の同期回数の削減という立場から従来の反復解法の効率について議論したい.ここで取り上げる反復法は,元の GPBiCG 法,GPBiCG_AR 法,そして,今回考案した GPBiCG_AR_β 法,GPBiCG_AR_β 法の合計 4 種類である.そして,これらの解法の反復 1 回当りの同期回数に着目し,それらの回数を減らすことに成功した.数値実験によって,これら …
NAID 110009675734

Transpose-AMIPの応用による気候システムの速い応答プロセスの解明

釜江陽一,渡部雅浩
週間及び1か月予報における顕著現象の予測可能性, 179-182, 2013-03
平成24年度京都大学防災研究所一般研究集会(24K-08)「週間及び1か月予報における顕著現象の予測可能性」, 京都大学防災研究所連携研究棟大セミナー室, 2012/11/20-22
NAID 120005244482

Computation-Communication Overlap Techniques for Parallel Spectral Calculations in Gyrokinetic Vlasov Simulations

MAEYAMA Shinya,WATANABE Tomohiko,IDOMURA Yasuhiro,NAKATA Motoki,NUNAMI Masanori,ISHIZAWA Akihiro
Plasma and Fusion Research 8(0), 1403150-1403150, 2013
… A key numerical technique is the parallel Fast Fourier Transform (FFT) required for parallel spectral calculations, where masking of the cost of inter-node transpose communications is essential to improve strong scaling. … To mask communication costs, computation-communication overlap techniques are applied for FFTs and transpose with the help of the hybrid parallelization of message passing interface and open multi-processing. …
NAID 130003392944

Breaking the performance bottleneck of sparse matrix-vector multiplication on SIMD processors

Zhang Kai,Chen Shuming,Wang Yaohua,Wan Jianghua
IEICE Electronics Express 10(9), 20130147-20130147, 2013
The low utilization of SIMD units and memory bandwidth is the main performance bottleneck on SIMD processors for sparse matrix-vector multiplication (SpMV), which is one of the most important kernels …
NAID 130003365022

Related Pictures

Description Matrix transpose dc.svg Transpose of a Matrix Transpose Software shot for transpose of matrix C program Based on the Excel spreadsheet above: Bad Suns / Transpose