- 英
- phase contrast, retardance?
- 同
- PC法
PrepTutorEJDIC
- Peace Corps 平和部隊
Wikipedia preview
出典(authority):フリー百科事典『ウィキペディア(Wikipedia)』「2013/12/28 14:58:09」(JST)
wiki ja
Japanese Journal
- 小型熱音響冷却システムにおけるスタック位置とヒートポンプ効果について
- 堀田 浩平,坂本 眞一,渡辺 好章
- 日本音響学会誌 67(4), 145-151, 2011-04-01
- … 本研究では,発振する音波の周波数が高くなるときの適切なヒートポンプの設置位置について無次元パラメータωτと音圧と粒子速度の位相差φに着目し検討を行った。 …
- NAID 110008593624
- ドライビングフィーリング評価のための車両・ドライバ挙動のパラメータ化に関する検討(研究速報)
- 福間 慎治,花井 雅典,佐藤 亮介,森 眞一郎,林 憲孝
- 電子情報通信学会論文誌. D, 情報・システム J94-D(4), 750-754, 2011-04-01
- … グ評価のための,自動車運転中のドライバと車両挙動の関係のパラメータ化について検討を行う.ドライバ挙動と車両挙動によるリサジュー曲線を近似し,近似係数からパラメータを求め,これをドライバが感じた「運転のしやすさ」と比較する.その結果,運転しやすい車両は,車両横加速度と顔の垂直方向の動きの間の振幅比は小さく,位相差は負の方向に大きくなる,すなわちリサジュー波形がU字型に近づく傾向が見られた. …
- NAID 110008593483
Related Links
- テンプレートを表示. 位相(いそう、英語:phase)は、波動などの周期的な現象において、 ひとつの周期中の位置を示す無次元量で、通常は角度(単位は「度」または「ラジアン」) で表される。 目次. 1 概要; 2 複素数による表現; 3 交流における位相; 4 関連項目 ...
Related Pictures
★リンクテーブル★
| リンク元 | 「PC」「retardance」 |
| 拡張検索 | 「位相差顕微法」「位相差顕微鏡観察」 |
| 関連記事 | 「位相」「差」 |
「PC」
- 後交連 posterior commissure
- 位相差 phase contrast
- プラストシアニン plastocyanin
- ペニシリン penicillin
- プロスタサイクリン prostacyclin
- 濃厚血小板 platelet concentrate
- 褐色細胞腫 pheochromocytoma
「retardance」
「位相差顕微法」
「位相差顕微鏡観察」
「位相」
「差」
- 英
- difference
- 関
- 相違、差異

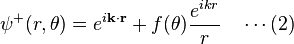

![\psi^+(r,\theta)
\to \sum_{l=0}^\infty \frac{(2l+1)}{2ik}\Big[(1+a_l)\frac{e^{ikr}}{r}-(-1)^l\frac{e^{-ikr}}{r}\Big]P_l(cos\theta)
\quad (r\to\infty)
\quad \cdots (4)](http://upload.wikimedia.org/math/a/e/1/ae1f2ac0e3d7ea02fdff7c18cd870b70.png)







