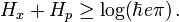uncertainty principle

• 不確定性原理

WordNet

1. not established beyond doubt; still undecided or unknown; "an uncertain future"; "a manuscript of uncertain origin"; "plans are still uncertain"; "changes of great if uncertain consequences"; "without further evidence his story must remain uncertain"
2. lacking or indicating lack of confidence or assurance; "uncertain of his convictions"; "unsure of himself and his future"; "moving with uncertain (or unsure) steps"; "an uncertain smile"; "touched the ornaments with uncertain fingers" (同)unsure, incertain
3. ambiguous (especially in the negative); "she spoke in no uncertain terms"
4. not certain to occur; not inevitable; "everything is uncertain about the army"; "the issue is uncertain"
5. not consistent or dependable; "an uncertain recollection of events"; "a gun with a rather uncertain trigger"
6. rule of personal conduct (同)precept
7. a basic generalization that is accepted as true and that can be used as a basis for reasoning or conduct; "their principles of composition characterized all their works" (同)rule
8. a rule or law concerning a natural phenomenon or the function of a complex system; "the principle of the conservation of mass"; "the principle of jet propulsion"; "the right-hand rule for inductive fields" (同)rule
9. a basic truth or law or assumption; "the principles of democracy"
10. a rule or standard especially of good behavior; "a man of principle"; "he will not violate his principles"
11. being unsettled or in doubt or dependent on chance; "the uncertainty of the outcome"; "the precariousness of his income" (同)uncertainness, precariousness
12. based on or manifesting objectively defined standards of rightness or morality; "principled pragmatism and unprincipled expediency"; "a principled person"

PrepTutorEJDIC

1. 《補語にのみ用いて》(人が)『確信が持てない』,はっきり分からない / (結果などが)『確かでない』,はっきりしない,疑わしい / 『変わりやすい』,不安定な / 明確でない,ぼんやりした
2. 〈C〉『原理,原則』;法則 / 〈C〉『主義,信条』,基本方針,行動指針 / 〈U〉道義,節繰
3. 〈U〉確信のなさ;疑わしさ;変わりやすさ;不明確さ / 〈C〉《しばしば複数形で》確信のない(疑わしい,変わりやすい,不明確な)こと
4. 「…主義の(をもった)」の意を表す

Wikipedia preview

出典(authority):フリー百科事典『ウィキペディア（Wikipedia）』「2012/04/19 15:51:36」(JST)

wiki en

[Wiki en表示]

For other uses, see Uncertainty principle (disambiguation).

Quantum mechanics
Uncertainty principle
Introduction Glossary · History
Background Bra-ket notation · Classical mechanics Hamiltonian · Interference Old quantum theory
Fundamental concepts Complementarity · Decoherence Duality · Ehrenfest theorem Entanglement · Exclusion Measurement · Probability amplitude Nonlocality · Quantum state Superposition · Tunnelling Uncertainty · Wave function
Experiments Bell's inequality · Davisson–Germer Delayed choice quantum eraser Double-slit · Elitzur–Vaidman Popper · Quantum eraser Schrödinger's cat · Stern–Gerlach Wheeler's delayed choice
Formulations Formulations Heisenberg · Interaction Matrix mechanics · Schrödinger Sum over histories
Equations Dirac · Klein–Gordon Pauli · Rydberg Schrödinger
Interpretations Interpretations (overview) Consciousness-caused Consistent histories Copenhagen · de Broglie–Bohm Ensemble · Hidden variables Many-worlds · Objective collapse Pondicherry · Quantum logic Relational · Stochastic Transactional
Advanced topics Quantum chaos · Quantum field theory Quantum information science Scattering theory
Scientists Bell · Bohm · Bohr · Born · Bose de Broglie · Dirac · Ehrenfest Everett · Feynman · Heisenberg Jordan · Kramers · von Neumann Pauli · Planck · Schrödinger Sommerfeld · Wien · Wigner

The wave function of an initially very localized particle

In quantum mechanics, the Heisenberg uncertainty principle states a fundamental limit on the accuracy with which certain pairs of physical properties of a particle, such as position and momentum, can be simultaneously known. In layman's terms, the more precisely one property is measured, the less precisely the other can be controlled, determined, or known.

In his Nobel Laureate speech, Max Born said:

“

...To measure space coordinates and instants of time, rigid measuring rods and clocks are required. On the other hand, to measure momenta and energies, devices are necessary with movable parts to absorb the impact of the test object and to indicate the size of its momentum. Paying regard to the fact that quantum mechanics is competent for dealing with the interaction of object and apparatus, it is seen that no arrangement is possible that will fulfill both requirements simultaneously...

”

Published by Werner Heisenberg in 1927, the uncertainty principle was a monumental discovery in the early development of quantum theory. It implies that it is impossible to simultaneously measure the present position while also determining the future motion of a particle, or of any system small enough to require quantum mechanical treatment.

The reason for the uncertainty principle arises from the differing eigenstates of non-commuting observables. The eigenstates of an observable represents the state of the wavefunction for a certain measurement value (the eigenvalue). For example, if a measurement of an observable is taken then the system is in a particular eigenstate of that observable. The particular eigenstate of the observable may not be an eigenstate of another observable . If this is so, then it does not have a single associated measurement as the system is not in an eigenstate of the observable.

Intuitively, the principle can be understood by considering a typical measurement of a particle. It is impossible to determine both momentum and position by means of the same measurement, as indicated by Born above. Assume that its initial momentum has been accurately calculated by measuring its mass, the force applied to it, and the length of time it was subjected to that force. Then to measure its position after it is no longer being accelerated would require another measurement to be done by scattering light or other particles off of it. But each such interaction will alter its momentum by an unknown and indeterminable increment, degrading our knowledge of its momentum while augmenting our knowledge of its position. So Heisenberg argues that every measurement destroys part of our knowledge of the system that was obtained by previous measurements. The uncertainty principle states a fundamental property of quantum systems, and is not a statement about the observational success of current technology.

The principle states specifically that the product of the uncertainties in position and momentum is always equal to or greater than one half of the reduced Planck constant ħ, which is defined as the re-scaling h/(2π) of the Planck constant h. Mathematically, the uncertainty relation between position and momentum arises because the expressions of the wavefunction in the two corresponding bases are Fourier transforms of one another (i.e., position and momentum are conjugate variables). In the mathematical formulation of quantum mechanics, any non-commuting operators are subject to similar uncertainty limits.

Historical introduction

Main article: Introduction to quantum mechanics

Werner Heisenberg formulated the Uncertainty Principle at Niels Bohr's institute in Copenhagen, while working on the mathematical foundations of quantum mechanics.

In 1925, following pioneering work with Hendrik Kramers, Heisenberg developed matrix mechanics, which replaced the ad-hoc old quantum theory with modern quantum mechanics. The central assumption was that the classical concept of motion does not fit at the quantum level, and that electrons in an atom do not travel on sharply defined orbits. Rather, the motion is smeared out in a strange way: the Fourier transform of time only involve those frequencies that could be seen in quantum jumps.

Heisenberg's paper did not admit any unobservable quantities like the exact position of the electron in an orbit at any time; he only allowed the theorist to talk about the Fourier components of the motion. Since the Fourier components were not defined at the classical frequencies, they could not be used to construct an exact trajectory, so that the formalism could not answer certain overly precise questions about where the electron was or how fast it was going.

The most striking property of Heisenberg's infinite matrices for position and momentum is that they do not commute. Heisenberg's canonical commutation relation indicates by how much:

(see derivations)

and this result did not have a clear physical interpretation in the beginning.

In March 1926, working in Bohr's institute, Heisenberg realized that the non-commutativity implies the uncertainty principle. This implication provided a clear physical interpretation for the non-commutativity, and it laid the foundation for what became known as the Copenhagen interpretation of quantum mechanics. Heisenberg showed that the commutation relation implies an uncertainty, or in Bohr's language a complementarity. Any two variables that do not commute cannot be measured simultaneously — the more precisely one is known, the less precisely the other can be known. Heisenberg wrote:

It can be expressed in its simplest form as follows: One can never know with perfect accuracy both of those two important factors which determine the movement of one of the smallest particles—its position and its velocity. It is impossible to determine accurately both the position and the direction and speed of a particle at the same instant.

One way to understand the complementarity between position and momentum is by wave-particle duality. If a particle described by a plane wave passes through a narrow slit in a wall like a water-wave passing through a narrow channel, the particle diffracts and its wave comes out in a range of angles. The narrower the slit, the wider the diffracted wave and the greater the uncertainty in momentum afterward. The laws of diffraction require that the spread in angle is about , where is the slit width and is the wavelength. Reasoning based on the de Broglie relation shows that the size of the slit and the range in momentum of the diffracted wave are related by Heisenberg's rule:

In his celebrated 1927 paper, "Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik" ("On the Perceptual Content of Quantum Theoretical Kinematics and Mechanics"), Heisenberg established this expression as the minimum amount of unavoidable momentum disturbance caused by any position measurement, but he did not give a precise definition for the uncertainties Δx and Δp. Instead, he gave some plausible estimates in each case separately. In his Chicago lecture he refined his principle:

Kennard in 1927 first proved the modern inequality:

where ħ = h/2π, and σ_x, σ_p are the standard deviations of position and momentum. Heisenberg himself only proved relation (2) for the special case of Gaussian states.

Terminology and translation

Throughout the main body of his original 1927 paper, written in German, Heisenberg used the word "Unbestimmtheit" ("indeterminacy") to describe the basic theoretical principle. Only in the endnote did he switch to the word "Unsicherheit" ("uncertainty"). However, when the English-language version of Heisenberg's textbook, The Physical Principles of the Quantum Theory, was published in 1930, the translation "uncertainty" was used, and it became the more commonly used term in the English language thereafter.

Heisenberg's microscope

Heisenberg's gamma-ray microscope for locating an electron (shown in blue). The incoming gamma ray (shown in green) is scattered by the electron up into the microscope's aperture angle θ. The scattered gamma-ray is shown in red. Classical optics shows that the electron position can be resolved only up to an uncertainty Δx that depends on θ and the wavelength λ of the incoming light.

Main article: Heisenberg's microscope

The principle is quite counter-intuitive, so the early students of quantum theory had to be reassured that naive measurements to violate it were bound to be always unworkable. One way in which Heisenberg originally illustrated the intrinsic impossibility of violating the uncertainty principle is by using an imaginary microscope as a measuring device.

He imagines an experimenter trying to measure the position and momentum of an electron by shooting a photon at it.

Problem 1 - If the photon has a short wavelength, and therefore a large momentum, the position can be measured accurately. But the photon scatters in a random direction, transferring a large and uncertain amount of momentum to the electron. If the photon has a long wavelength and low momentum, the collision does not disturb the electron's momentum very much, but the scattering will reveal its position only vaguely.

Problem 2 - If a large aperture is used for the microscope, the electron's location can be well resolved (see Rayleigh criterion); but by the principle of conservation of momentum, the transverse momentum of the incoming photon and hence the new momentum of the electron resolves poorly. If a small aperture is used, the accuracy of both resolutions is the other way around.

The combination of these trade-offs imply that no matter what photon wavelength and aperture size are used, the product of the uncertainty in measured position and measured momentum is greater than or equal to a lower limit, which is (up to a small numerical factor) equal to Planck's constant. Heisenberg did not care to formulate the uncertainty principle as an exact limit (which is elaborated below), and preferred to use it instead as a heuristic quantitative statement, correct up to small numerical factors, which makes the radically new noncommutativity of quantum mechanics inevitable.

Critical reactions

Main article: Bohr–Einstein debates

The Copenhagen interpretation of quantum mechanics and Heisenberg's Uncertainty Principle were in fact seen as twin targets by detractors who believed in an underlying determinism and realism. According to the Copenhagen interpretation of quantum mechanics, there is no fundamental reality that the quantum state describes, just a prescription for calculating experimental results. There is no way to say what the state of a system fundamentally is, only what the result of observations might be.

Albert Einstein believed that randomness is a reflection of our ignorance of some fundamental property of reality, while Niels Bohr believed that the probability distributions are fundamental and irreducible, and depend on which measurements we choose to perform. Einstein and Bohr debated the uncertainty principle for many years.

Einstein's slit

The first of Einstein's thought experiments challenging the uncertainty principle went as follows:

Consider a particle passing through a slit of width d. The slit introduces an uncertainty in momentum of approximately h/d because the particle passes through the wall. But let us determine the momentum of the particle by measuring the recoil of the wall. In doing so, we find the momentum of the particle to arbitrary accuracy by conservation of momentum.

Bohr's response was that the wall is quantum mechanical as well, and that to measure the recoil to accuracy the momentum of the wall must be known to this accuracy before the particle passes through. This introduces an uncertainty in the position of the wall and therefore the position of the slit equal to , and if the wall's momentum is known precisely enough to measure the recoil, the slit's position is uncertain enough to disallow a position measurement.

A similar analysis with particles diffracting through multiple slits is given by Richard Feynman.

Einstein's box

Bohr was present when Einstein proposed the thought experiment which has become known as Einstein's box. Einstein argued that "Heisenberg's uncertainty equation implied that the uncertainty in time was related to the uncertainty in energy, the product of the two being related to Planck's constant." Consider, he said, an ideal box, lined with mirrors so that it can contain light indefinitely. The box could be weighed before a clockwork mechanism opened an ideal shutter at a chosen instant to allow one single photon to escape. "We now know, explained Einstein, precisely the time at which the photon left the box." "Now, weigh the box again. The change of mass tells the energy of the emitted light. In this manner, said Einstein, one could measure the energy emitted and the time it was released with any desired precision, in contradiction to the uncertainty principle."

Bohr spent a sleepless night considering this argument, and eventually realized that it was flawed. He pointed out that if the box were to be weighed, say by a spring and a pointer on a scale, "since the box must move vertically with a change in its weight, there will be uncertainty in its vertical velocity and therefore an uncertainty in its height above the table. ... Furthermore, the uncertainty about the elevation above the earth's surface will result in an uncertainty in the rate of the clock," because of Einstein's own theory of gravity's effect on time. "Through this chain of uncertainties, Bohr showed that Einstein's light box experiment could not simultaneously measure exactly both the energy of the photon and the time of its escape."

EPR paradox for entangled particles

Bohr was compelled to modify his understanding of the uncertainty principle after another thought experiment by Einstein. In 1935, Einstein, Podolsky and Rosen (see EPR paradox) published an analysis of widely separated entangled particles. Measuring one particle, Einstein realized, would alter the probability distribution of the other, yet here the other particle could not possibly be disturbed. This example led Bohr to revise his understanding of the principle, concluding that the uncertainty was not caused by a direct interaction.

But Einstein came to much more far-reaching conclusions from the same thought experiment. He believed the "natural basic assumption" that a complete description of reality would have to predict the results of experiments from "locally changing deterministic quantities", and therefore would have to include more information than the maximum possible allowed by the uncertainty principle.

In 1964 John Bell showed that this assumption can be falsified, since it would imply a certain inequality between the probabilities of different experiments. Experimental results confirm the predictions of quantum mechanics, ruling out Einstein's basic assumption that led him to the suggestion of his hidden variables. (Ironically this fact is one of the best pieces of evidence supporting Karl Popper's philosophy of invalidation of a theory by falsification-experiments. That is to say, here Einstein's "basic assumption" became falsified by experiments based on Bell's inequalities. For the objections of Karl Popper against the Heisenberg inequality itself, see below.)

While it is possible to assume that quantum mechanical predictions are due to nonlocal hidden variables, and in fact David Bohm invented such a formulation, this resolution is not satisfactory to the vast majority of physicists. The question of whether a random outcome is predetermined by a nonlocal theory can be philosophical, and it can be potentially intractable. If the hidden variables are not constrained, they could just be a list of random digits that are used to produce the measurement outcomes. To make it sensible, the assumption of nonlocal hidden variables is sometimes augmented by a second assumption — that the size of the observable universe puts a limit on the computations that these variables can do. A nonlocal theory of this sort predicts that a quantum computer encounters fundamental obstacles when it tries to factor numbers of approximately 10,000 digits or more; an achievable task in quantum mechanics.

Popper's criticism

Main article: Popper's experiment

Karl Popper approached the problem of indeterminacy as a logician and metaphysical realist. He disagreed with the application of the uncertainty relations to individual particles rather than to ensembles of identically prepared particles, referring to them as "statistical scatter relations". In this statistical interpretation, a particular measurement may be made to arbitrary precision without invalidating the quantum theory. This directly contrasts the Copenhagen interpretation of quantum mechanics, which is non-deterministic but lacks local hidden variables.

In 1934 Popper published Zur Kritik der Ungenauigkeitsrelationen (Critique of the Uncertainty Relations) in Naturwissenschaften, and in the same year Logik der Forschung (translated and updated by the author as The Logic of Scientific Discovery in 1959), outlining his arguments for the statistical interpretation. In 1982, he further developed his theory in Quantum theory and the schism in Physics, writing:

[Heisenberg's] formulae are, beyond all doubt, derivable statistical formulae of the quantum theory. But they have been habitually misinterpreted by those quantum theorists who said that these formulae can be interpreted as determining some upper limit to the precision of our measurements.[original emphasis]

Popper proposed an experiment to falsify the uncertainty relations, though he later withdrew his initial version after discussions with Weizsäcker, Heisenberg, and Einstein; this experiment may have influenced the formulation of the EPR experiment.

Many-worlds uncertainty

Main article: Many-worlds interpretation

The many-worlds interpretation originally outlined by Hugh Everett III in 1957 is partly meant to reconcile the differences between the Einstein and Bohr's views by replacing Bohr's wave function collapse with an ensemble of deterministic and independent universes whose distribution is governed by wave functions and the Schrödinger equation. Thus, uncertainty in the many-worlds interpretation follows from each observer within any universe having no knowledge of what goes on in the other universes.

Matter wave interpretation

Main article: Wave packet

According to the de Broglie hypothesis, every object in our Universe is a wave, a situation which gives rise to this phenomenon. Consider the measurement of the position of a particle. The particle's wave packet has non-zero amplitude, meaning that the position is uncertain – it could be almost anywhere along the wave packet. To obtain an accurate reading of position, this wave packet must be 'compressed' as much as possible, meaning it must be made up of increasing numbers of sine waves added together. The momentum of the particle is proportional to the wavenumber of one of these waves, but it could be any of them. So a more precise position measurement – by adding together more waves – means that the momentum measurement becomes less precise (and vice versa).

The only kind of wave with a definite position is concentrated at one point, and such a wave has an indefinite wavelength (and therefore an indefinite momentum). Conversely, the only kind of wave with a definite wavelength is an infinite regular periodic oscillation over all space, which has no definite position. So in quantum mechanics, there can be no states that describe a particle with both a definite position and a definite momentum. The more precise the position, the less precise the momentum.

A mathematical statement of the principle is that every quantum state has the property that the root mean square (RMS) deviation of the position from its mean (the standard deviation of the x-distribution):

times the RMS deviation of the momentum from its mean (the standard deviation of p):

can never be smaller than a fixed fraction of Planck's constant:

The uncertainty principle can be restated in terms of other measurement processes, which involves collapse of the wavefunction. When the position is initially localized by preparation, the wavefunction collapses to a narrow bump in an interval Δx > 0, and the momentum wavefunction becomes spread out (cf. wave packet). The particle's momentum is left uncertain by an amount inversely proportional to the accuracy of the position measurement:

.

If the initial preparation in Δx is understood as an observation or disturbance of the particles then this means that the uncertainty principle is related to the observer effect. However, this is not true in the case of the measurement process corresponding to the former inequality but only for the latter inequality.

Additional uncertainty relations

Further information: Uncertainty Principle Derivations

The Heisenberg uncertainty relation and its more formal versions deal explicitly with the quantum operators for position, and for momentum, . Uncertainty relations for generalized operators have also been derived, such as the Robertson uncertainty relation and for arbitrary Hermitian operators and is given by

A further generalization of the Robertson relation was derived by Schrödinger to give

Since the Robertson and Schrödinger relations are for general operators, then they can be used to obtain uncertainty relations for any two observables that do not commute. Examples include:

• The kinetic energy and position of a particle :

• For two orthogonal components of the total angular momentum operator of an object:

where i, j, k are distinct and J_i denotes angular momentum along the x_i axis. This relation implies that only a single component of a system's angular momentum can be defined with arbitrary precision, normally the component parallel to an external (magnetic or electric) field. Moreover, for , a choice , in angular momentum multiplets, ψ = |j, m 〉, bounds the Casimir invariant (angular momentum squared, ) from below and thus yields useful constraints such as j (j+1) ≥ m (m + 1), and hence j ≥ m, among others.

• For the number of electrons in a superconductor and the phase of its Ginzburg–Landau order parameter

Energy–time uncertainty principle

Other than the position-momentum uncertainty relation, the most important uncertainty relation is that between energy and time. The energy-time uncertainty relation is not, however, an obvious consequence of the general Robertson–Schrödinger relation. Since energy bears the same relation to time as momentum does to space in special relativity, it was clear to many early founders, Niels Bohr among them, that the following relation should hold:

but it was not always obvious what precisely meant. The problem is that the time at which the particle has a given state is not an operator belonging to the particle, it is a parameter describing the evolution of the system. As Lev Landau once joked "To violate the time-energy uncertainty relation all I have to do is measure the energy very precisely and then look at my watch!"

Nevertheless, Einstein and Bohr understood the heuristic meaning of the principle. A state that only exists for a short time cannot have a definite energy. To have a definite energy, the frequency of the state must accurately be defined, and this requires the state to hang around for many cycles, the reciprocal of the required accuracy.

For example, in spectroscopy, excited states have a finite lifetime. By the time-energy uncertainty principle, they do not have a definite energy, and each time they decay the energy they release is slightly different. The average energy of the outgoing photon has a peak at the theoretical energy of the state, but the distribution has a finite width called the natural linewidth. Fast-decaying states have a broad linewidth, while slow decaying states have a narrow linewidth.

The broad linewidth of fast decaying states makes it difficult to accurately measure the energy of the state, and researchers have even used detuned microwave cavities to slow down the decay-rate, to get sharper peaks. The same linewidth effect also makes it difficult to measure the rest mass of fast decaying particles in particle physics. The faster the particle decays, the less certain is its mass.

One false formulation of the energy-time uncertainty principle says that measuring the energy of a quantum system to an accuracy requires a time interval . This formulation is similar to the one alluded to in Landau's joke, and was explicitly invalidated by Y. Aharonov and D. Bohm in 1961 . The time in the uncertainty relation is the time during which the system exists unperturbed, not the time during which the experimental equipment is turned on, whereas the position in the other version of the principle refers to where the particle has some probability to be and not where the observer might look.

Another common misconception is that the energy-time uncertainty principle says that the conservation of energy can be temporarily violated – energy can be "borrowed" from the Universe as long as it is "returned" within a short amount of time. Although this agrees with the spirit of relativistic quantum mechanics, it is based on the false axiom that the energy of the Universe is an exactly known parameter at all times. More accurately, when events transpire at shorter time intervals, there is a greater uncertainty in the energy of these events. Therefore it is not that the conservation of energy is violated when quantum field theory uses temporary electron-positron pairs in its calculations, but that the energy of quantum systems is not known with enough precision to limit their behavior to a single, simple history. Thus the influence of all histories must be incorporated into quantum calculations, including those with much greater or much less energy than the mean of the measured/calculated energy distribution.

In 1932 Dirac offered a precise definition and derivation of the time-energy uncertainty relation in a relativistic quantum theory of "events". But a better-known, more widely used formulation of the time-energy uncertainty principle was given in 1945 by L. I. Mandelshtam and I. E. Tamm, as follows. For a quantum system in a non-stationary state and an observable represented by a self-adjoint operator , the following formula holds:

where is the standard deviation of the energy operator in the state , stands for the standard deviation of . Although, the second factor in the left-hand side has dimension of time, it is different from the time parameter that enters Schrödinger equation. It is a lifetime of the state with respect to the observable . In other words, this is the time after which the expectation value changes appreciably.

Entropic uncertainty principle

Main article: Hirschman uncertainty

While formulating the many-worlds interpretation of quantum mechanics in 1957, Hugh Everett III discovered a much stronger formulation of the uncertainty principle. In the inequality of standard deviations, some states, like the wavefunction

$\psi(x) \propto e^{-\frac{x^2}{0.0001}}+ e^{- \frac{(x-100)^2}{0.0001 }}$

have a large standard deviation of position, but are actually a superposition of very narrow bumps. In this case, the momentum uncertainty is much larger than the above Robertson inequality would suggest, in fact σ_xσ_p ~ 10000ħ, so very far from saturation. (The above stronger Schrödinger inequality, however, does better.)

A tighter inequality uses the Shannon entropy of the distribution, a measure of the uncertainty in a random variable described by a probability distribution,

$H_x = - \int |\psi(x)|^2 \log_n |\psi(x)|^2 \,dx ~,$

where n is an arbitrary base for the logarithm. The interpretation of H_x is that, for example if n=2, it is the number of bits of information an observer acquires when the value of x is given to accuracy ε is equal to I_x + log₂(ε). The second part is just the number of bits past the decimal point, while the first part is a logarithmic measure of the width of the distribution. For a uniform distribution of width Δx, the information content is log₂Δx bits. (This quantity can be negative, which means that the distribution is narrower than one unit, so that learning the first few bits past the decimal point gives no information, since they are not uncertain.)

For |ψ(x)|² a normalized Gaussian, this entropy amounts to the variance discussed above, cf. Shannon's inequalities. For a fixed variance σ_x, the Gaussian maximizes the entropy, so that H ≤ ½ log (2πeσ²), Shannon's inequality.

Everett (and Hirschman) conjectured that for all quantum states:

$H_x + H_p \ge \log (\hbar e\pi)\, .$

This was proven in more detail by Beckner and by Iwo Bialynicki-Birula and Jerzy Mycielski in 1975. The inequality is saturated when |ψ(x)|² is a normalized Gaussian.

Exponentiating Shannon's inequality for a given distribution with variance σ_x, and for its momentum (Fourier conjugate) distribution with variance σ_p, and combining with the above entropic inequality yields

2 eπ σ_xσ_p ≥ exp (H_x+H_y) ≥ eπ .

Evidently, the entropic inequality, since it implies the conventional (variance) inequality, is tighter.

Harmonic analysis

In the context of harmonic analysis, a branch of mathematics, the uncertainty principle implies that one cannot at the same time localize the value of a function and its Fourier transform. To wit, the following inequality holds:

Other purely mathematical formulations of uncertainty exist between a function f and its Fourier transform – see Fourier transform#Uncertainty principle. A variety of such results can be found in (Havin & Jöricke 1994) or (Folland & Sitaram 1997); for a short survey, see (Sitaram 2001).

Signal processing

In the context of signal processing, particularly time–frequency analysis, uncertainty principles are referred to as the Gabor limit, after Dennis Gabor, or sometimes the Heisenberg–Gabor limit. The basic result, which follows from Benedicks's theorem, below, is that a function cannot be both time limited and band limited (a function and its Fourier transform cannot both have bounded domain) – see bandlimited versus timelimited. Stated alternatively, "one cannot simultaneously localize a signal (function) in both the time domain (f) and frequency domain (Fourier transform)". When applied to filters, the result is that one cannot achieve high temporal resolution and frequency resolution at the same time; a concrete example are the resolution issues of the short-time Fourier transform – if one uses a wide window, one achieves good frequency resolution at the cost of temporal resolution, while a narrow window has the opposite trade-off.

Alternative theorems give more precise quantitative results, and in time–frequency analysis, rather than interpreting the (1-dimensional) time and frequency domains separately, one instead interprets the limit as a lower limit on the support of a function in the (2-dimensional) time–frequency plane. In practice the Gabor limit limits the simultaneous time–frequency resolution one can achieve without interference; it is possible to achieve higher resolution, but at the cost of different components of the signal interfering with each other.

Benedicks's theorem

Amrein-Berthier (Amrein & Berthier 1977) and Benedicks's theorem (Benedicks 1985) intuitively says that the set of points where f is non-zero and the set of points where is nonzero cannot both be small. Specifically, it is impossible for a function f in L²(R) and its Fourier transform to both be supported on sets of finite Lebesgue measure. A more quantitative version is due to Nazarov (Nazarov 1994) and (Jaming 2007):

One expects that the factor may be replaced by which is only known if either or is convex.

Hardy's uncertainty principle

The mathematician G. H. Hardy (Hardy 1933) formulated the following uncertainty principle: it is not possible for f and to both be "very rapidly decreasing." Specifically, if f is in L²(R), is such that

and

( an integer)

then, if while if then there is a polynomial of degree such that

This was later improved as follows: if is such that

then

where is a polynomial of degree and is a real positive definite matrix.

This result was stated in Beurling's complete works without proof and proved in Hörmander (Hörmander 1991) (the case ) and Bonami–Demange–Jaming (Bonami, Demange & Jaming 2003) for the general case. Note that Hörmander–Beurling's version implies the case in Hardy's Theorem while the version by Bonami–Demange–Jaming covers the full strength of Hardy's Theorem.

A full description of the case as well as the following extension to Schwarz class distributions appears in Demange (Demange 2010):

Theorem. If a tempered distribution is such that

and

then

for some convenient polynomial and real positive definite matrix of type .

See also

• Canonical commutation relation
• Correspondence principle
• Correspondence rules
• Gromov's non-squeezing theorem
• Heisenbug

• Introduction to quantum mechanics
• Observer effect (information technology)
• Observer effect (physics)
• Quantum indeterminacy
• The Part and The Whole (book)

Notes

References

• Amrein, W.O.; Berthier, A.M. (1977), "On support properties of L^p-functions and their Fourier transforms", Journal of Functional Analysis 24 (3): 258–267, doi:10.1016/0022-1236(77)90056-8. 
• Benedicks, M. (1985), "On Fourier transforms of functions supported on sets of finite Lebesgue measure", J. Math. Anal. Appl. 106 (1): 180–183, doi:10.1016/0022-247X(85)90140-4 .
• Benedicks, M. (1985), "On Fourier transforms of functions supported on sets of finite Lebesgue measure", J. Math. Anal. Appl. 106 (1): 180–183, doi:10.1016/0022-247X(85)90140-4 .
• Bonami, A.; Demange, B.; Jaming, Ph. (2003), "Hermite functions and uncertainty principles for the Fourier and the windowed Fourier transforms", Rev. Mat. Iberoamericana 19: 23–55. .
• Folland, Gerald; Sitaram, Alladi (May 1997), "The Uncertainty Principle: A Mathematical Survey" (PDF), Journal of Fourier Analysis and Applications 3 (3): 207–238, doi:10.1007/BF02649110, MR98f:42006, http://www.springerlink.com/content/f7492v6374716m4g/fulltext.pdf 
• Hardy, G.H. (1933), "A theorem concerning Fourier transforms", J. London Math. Soc. 8 (3): 227–231, doi:10.1112/jlms/s1-8.3.227 .
• Havin, V.; Jöricke, B. (1994), The Uncertainty Principle in Harmonic Analysis, Springer-Verlag .
• Heisenberg, W. (1927), "Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik", Zeitschrift für Physik 43 (3–4): 172–198, Bibcode 1927ZPhy...43..172H, doi:10.1007/BF01397280 . English translation: J. A. Wheeler and H. Zurek, Quantum Theory and Measurement Princeton Univ. Press, 1983, pp. 62–84.
• Hörmander, L. (1991), "A uniqueness theorem of Beurling for Fourier transform pairs", Ark. Mat. 29: 231–240 .
• Jaming, Ph. (2007), "Nazarov's uncertainty principles in higher dimension", J. Approx. Theory 149 (1): 30–41, doi:10.1016/j.jat.2007.04.005 .
• Mandelshtam, Leonid; Tamm, Igor (1945), "The uncertainty relation between energy and time in nonrelativistic quantum mechanics", Izv. Akad. Nauk SSSR (ser. Fiz.) 9: 122–128, http://daarb.narod.ru/mandtamm/index-eng.html . English translation: J. Phys. (USSR) 9, 249–254 (1945).
• Nazarov, F. (1994), "Local estimates for exponential polynomials and their applications to inequalities of the uncertainty principle type,", St. Petersburg Math. J. 5: 663–717 .
• Sitaram, A (2001), "Uncertainty principle, mathematical", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=U/u130020 .

External links

• Annotated pre-publication proof sheet of Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik, March 23, 1927.
• Matter as a Wave – a chapter from an online textbook
• Quantum mechanics: Myths and facts
• Stanford Encyclopedia of Philosophy entry
• Fourier Transforms and Uncertainty at MathPages
• aip.org: Quantum mechanics 1925–1927 – The uncertainty principle
• Eric Weisstein's World of Physics – Uncertainty principle
• John Baez on the time-energy uncertainty relation

UpToDate Contents

全文を閲覧するには購読必要です。 To read the full text you will need to subscribe.

• 1. アスリートにおけるオーバートレーニング症候群 overtraining syndrome in athletes
• 2. 集中治療室（ICU）における成人に対する人工呼吸器によるサポートの休止および離脱 withholding and withdrawing ventilatory support in adults in the intensive care unit
• 3. 終末期の効果的な疼痛マネージメントにおける倫理的問題 ethical considerations in effective pain management at the end of life
• 4. 緩和ケアにおける倫理的問題 ethical issues in palliative care
• 5. ICUにおけるコミュニケーション：家族会議を開く communication in the icu holding a family meeting

English Journal

• The role of uncertainty and subjective influences on consequence assessment by aquatic biosecurity experts.

• Davidson AD, Campbell ML, Hewitt CL.SourceAustralian Maritime College, University of Tasmania, Locked Bay 1396, Launceston, TAS 7250, Australia. Electronic address: alisha.dahlstrom@gmail.com.
• Journal of environmental management.J Environ Manage.2013 Sep 30;127:103-13. doi: 10.1016/j.jenvman.2013.03.043. Epub 2013 May 17.
• Expert judgement is often used to mitigate the knowledge gaps that limit understanding of aquatic non-indigenous species (ANS) impacts (consequences) to environmental, economic, social, cultural and human health values. To understand how this uncertainty may affect expert decision making, we explore
• PMID 23685271

• The information-divergence hypothesis of informational masking.

• Lutfi RA, Gilbertson L, Heo I, Chang AC, Stamas J.SourceAuditory Behavioral Research Lab, Department of Communication Sciences and Disorders, University of Wisconsin, Madison, Wisconsin 53706.
• The Journal of the Acoustical Society of America.J Acoust Soc Am.2013 Sep;134(3):2160-70. doi: 10.1121/1.4817875.
• In recent years there has been growing interest in masking that cannot be attributed to interactions in the cochlea-so-called informational masking (IM). Similarity in the acoustic properties of target and masker and uncertainty regarding the masker are the two major factors identified with IM. Thes
• PMID 23967946

• A model of radiation-induced cell killing: insights into mechanisms and applications for hadron therapy.

• Ballarini F, Altieri S, Bortolussi S, Giroletti E, Protti N.SourceUniversity of Pavia, Physics Department, and INFN - Sezione di Pavia, via Bassi 6, I-27100 Pavia, Italy.
• Radiation research.Radiat Res.2013 Sep;180(3):307-15. doi: 10.1667/RR3285.1. Epub 2013 Aug 14.
• A mechanism-based, two-parameter biophysical model of cell killing was developed with the aim of elucidating the mechanisms underlying radiation-induced cell death and predicting cell killing by different radiation types, including protons and carbon ions at energies and doses of interest for cancer
• PMID 23944606

Japanese Journal

• 'Open-loop' tracking interferometer for machine tool volumetric error measurement --Two-dimensional case

• Ibaraki Soichi,Sato Goh,Takeuchi Kunitaka
• Precision Engineering 38(3), 666-672, 2014-07
• … Applying the multilateration principle, it measures the target's three-dimensional position at an arbitrary location in the workspace. … The objective of this paper is to validate this 'open-loop' tracking interferometer concept by investigating its measurement uncertainty both experimentally and analytically. …
• NAID 120005439528

• 論争問題学習における授業構成原理の「熟議的転回」 : National Issues Forumsの分析を通して

• 長田 健一
• 社会科研究 (80), 81-92, 2014-03-31
• 本研究は,わが国で提起された主な論争問題学習論に対し,それらの課題を乗り越える方途を「熟議」による論争問題学習が示していること,また,両者の間に授業構成原理上どのような「転回」が認められるのかを明らかにすることを目的とする。近年の社会学や政治学の有力な諸理論が示すように,「不確実性」を特徴とする現代社会では,個人の合理的意思決定や普遍的観点からの判断は困難となっている。それゆえ,合理性や普遍性に依 …
• NAID 110009810584

• 我々は意思決定能力を欠いた患者の治療拒否を尊重すべきか

• 浅井 篤,石本 博子
• 先端倫理研究 : 熊本大学倫理学研究室紀要 8, 25-35, 2014-03
• … What principle or reason could justify compulsory interventions against the patients' will? … Issues discussed would include standard treatments at a given time in a given culture, advance directives, perpetuity of incompetency, nature of refusedinterventions, alternatives, emergency, ethical and medical uncertainty, ourdiscriminatory feeling, human dignity, fundamental liberty, and patient's moralobligations. …
• NAID 110009687674

Related Links

• Uncertainty principle

The Uncertainty Principle The position and momentum of a particle cannot be simultaneously measured with arbitrarily high precision. There is a minimum for the product of the uncertainties of these two measurements. There is ...

• uncertainty principleの意味 - goo辞書 英和和英

uncertainty principleとは。意味や和訳。《物理学》不確定性原理. - 40万項目以上収録、例文・コロケーションが豊富な無料英和和英辞典。 ... プロバイダならOCN

---

★リンクテーブル★

リンク元	「不確定性原理」
関連記事	「uncertain」「principle」

「不確定性原理」

　　[★]

英

[[]]

同

uncertainty principle

関

[[]]

同

uncertainty principle

「uncertain」

　　[★]

• adj.

• 不確かな、未定の、不明な、不確定の、不確実な

関

equivocal、inconclusive、indefinite、indefinitely、indeterminate、not clear、obscure、uncertainly、unclear、unclearly、undecided、unexplained、unfixed、unidentified、unknown、unrevealing

　 　 　 　 　 　

「principle」

　　[★]

• n.

• 原理、原則、信条

関

belief、fundamentals、philosophy、rationale