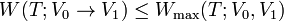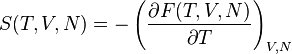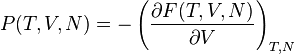自由エネルギー

英

free energy

関

エネルギー

Wikipedia preview

出典(authority):フリー百科事典『ウィキペディア（Wikipedia）』「2013/04/19 17:15:02」(JST)

wiki ja

[Wiki ja表示]

統計力学

熱力学 · 気体分子運動論

粒子統計 マクスウェル＝ボルツマン ボース＝アインシュタイン フェルミ＝ディラック パラ · エニオン · 組み紐 アンサンブル ミクロカノニカルアンサンブル カノニカルアンサンブル グランドカノニカルアンサンブル 等温‐等圧 等エントロピー‐等圧 熱力学 気体の法則 · カルノーサイクル デュロン＝プティの法則 模型 デバイ · アインシュタイン · イジング ポテンシャル 内部エネルギー エンタルピー ヘルムホルツの自由エネルギー ギブズの自由エネルギー グランドポテンシャル 科学者 マクスウェル · ギブズ · ボルツマン · アインシュタイン · オンサーガー · ウィルソン · 久保亮五 · カダノフ · フィッシャー · 川崎恭治 · パリジ · エドワーズ · ローレンツ · 蔵本由紀 · ジャルジンスキー · 西森秀稔 · 田崎晴明

自由エネルギー（じゆうエネルギー、free energy）とは、熱力学における状態量の1つである。熱力学第一法則から導いた式によりエネルギーの収支を、第二法則から得た式によりある過程の進行の自発性を扱えるので、十分な物理量を得るという意味でどんな状況をも物理および化学において取り扱える。ただし、実際の応用において便利な式とは、外界の（エントロピーなどの）変化まで計算・計測しなければ使えない式ではない。通常、関心がもたれるのは系で何が起きたかであり、外界の変化は重要ではない。自由エネルギーはある系内における熱力学的関数の変化による平衡と自発性の指標である

等温等積過程の自由エネルギーはヘルムホルツの自由エネルギー（Helmholtz free energy）と呼ばれ、等温等圧過程の自由エネルギーはギブズの自由エネルギー（Gibbs free energy）と呼ばれる。通常、ヘルムホルツ自由エネルギーはで表記され、ギブズ自由エネルギーはで表記される。体積変化が系外に為す仕事の分だけ異なるので両者の間にはの関係にある。

自由エネルギーは1882年にヘルマン・フォン・ヘルムホルツが提唱した熱力学上の概念で、呼称は彼の命名による。一方、等温等圧過程の自由エネルギーと化学ポテンシャルとの研究はウィラード・ギブズにより理論展開されたので、等温等積過程をヘルムホルツ自由エネルギーと等温等圧過程をギブズ自由エネルギーと呼び分ける。

熱力学第二法則より、系は自由エネルギーが減少する方向に進行する。また、閉じた系における熱平衡条件は自由エネルギーが極小値をとることである。

ヘルムホルツの自由エネルギー

ヘルムホルツエネルギー（Helmholtz free energy)は熱力学における示量性状態量のひとつで、等温条件で取り出し可能なエネルギー量をいう。記号 F や A で表されることが多い。

内部エネルギー U、温度 T、エントロピー S を用いて、

で定義される。

内部エネルギーをエントロピー S、体積 V、物質量 N の関数 U(S,V,N) としてみたとき、温度 T、体積 V、物質量 N の関数としてみたヘルムホルツエネルギー F(T,V,N) は S に関するルジャンドル変換

と見ることができる。

「熱力学ポテンシャル」も参照

等温過程

ヘルムホルツエネルギーは等温条件において取り出し可能な仕事量である。 温度 T の環境にある系が体積 V₀ から V₁ へと変化する際に外部にした仕事を W とするとこの仕事には上限が存在する。

$W(T; V_0 \to V_1) \le W_\mathrm{max}(T;V_0,V_1)$

ヘルムホルツエネルギーを用いると、

と表される。 ヘルムホルツエネルギーの減少量が取り出し可能な仕事量となる。

熱力学第二法則

系が温度 T_ex の外界と熱的平衡にあるとき、熱力学第二法則から、系に変化が起こるとき

である。 一方、エネルギー保存則から

であるが、体積一定の条件下 では第二項は 0 となる。 従って、

であるが、系は外界と熱平衡状態にあるため、系の温度は外界の温度と等しく 、温度が一定 なので

となる。

等温等積の条件下では、自発変化はヘルムホルツエネルギーが減少する方向へ進む。また熱平衡条件はヘルムホルツエネルギーが極小値をとることである。

微分

F(T,V,N) の全微分は次の形になる。

ここで、Pは圧力、は各成分の化学ポテンシャルを表す。 従って、偏微分はそれぞれ

$S(T,V,N) = -\left( \frac{\partial F(T,V,N)}{\partial T} \right)_{V,N}$

$P(T,V,N) = -\left( \frac{\partial F(T,V,N)}{\partial V} \right)_{T,N}$

$\mu_i(T,V,N) = \left( \frac{\partial F(T,V,N)}{\partial N_i} \right)_{T,V}$

となる。

系のスケール変換を考えると、

の関係が得られる。

統計力学との関係

統計力学では、カノニカルアンサンブルと関係付けられる。 分配関数 を用いて、

と表される。 これはミクロとマクロをつなぐボルツマンの関係

から導かれる。

ギブズの自由エネルギー

ギブズ自由エネルギー（Gibbs free energy）は、熱力学や電気化学などで用いられ、エネルギーの次元をもつ示量性状態量である。ちなみにIUPACではギブズエネルギーという名称の使用を勧告している。 記号 G と表されることが多く、等温等圧条件下で仕事として取り出し可能なエネルギー量である。

ギブズ自由エネルギーは自発的に減少しようとする。即ち、Gの変化が負であれば化学反応は自発的に起こる。さらに、ギブスエネルギーが極小の一定値を取ることは系が平衡状態にあることに等しい。

これは、ヘルムホルツの自由エネルギーに関する

ヘルムホルツの自由エネルギーは自発的に減少しようとする。即ち、Fの変化が負であれば化学反応は自発的に起こる。さらに、ヘルムホルツの自由エネルギーが極小の一定値を取ることは系が平衡状態にあることに等しい。

と対応している。違いは、系内が等温条件のみであるか、あるいは等温等圧条件であるかである。

ギブズエネルギーはエンタルピー H、温度 T、エントロピー S を用いて

で定義される。

エンタルピーをエントロピー S、圧力 P、物質量 N の関数 H(S,p,N) としてみたとき、温度 T、圧力 P、物質量 N の関数としてみたギブズエネルギー G(T,P,N) は S に関するルジャンドル変換

と見ることができる。

あるいは、ヘルムホルツエネルギー F、 圧力 P、体積 V を用いて

で定義されることもある。

このときは V に関するルジャンドル変換

と見ることができる。

エンタルピーの定義 H = U + PV 、或いはヘルムホルツエネルギーの定義 F = U - TS（U は内部エネルギーを表す）より以下の式を得ることができる。

系が温度 T_ex 、圧力 p_ex の外界と熱的平衡にあるとき、熱力学第二法則から、系に変化が起こるとき、前節と同様に

となる。 系は外界と熱平衡状態にあるため、系の温度と圧力は一定で外界と等しいので、

となる。

等温等圧の条件下では、自発変化はギブズエネルギーが減少する方向へ進む。また熱平衡条件はギブズエネルギーが極小値をとることである。

微分

G(T,P,N) の全微分は次の形になる。

ここで、 は各成分の化学ポテンシャルを表す。 従って、偏微分はそれぞれ

$S(T,P,N) = -\left( \frac{\partial G(T,P,N)}{\partial T} \right)_{P,N}$

$V(T,P,N) = \left( \frac{\partial G(T,P,N)}{\partial P} \right)_{T,N}$

$\mu_i(T,P,N) = \left( \frac{\partial G(T,P,N)}{\partial N_i} \right)_{T,P,N}$

となる。

系のスケール変換を考えると、

の関係が得られる。

平衡定数との関係

定圧定温条件での化学反応におけるギブズ自由エネルギー変化はエンタルピー変化およびエントロピー変化と以下の関係がある。

ギブズ自由エネルギー変化と平衡定数Kとの間には以下のような関係がある。ここで R は気体定数である。

標準状態（25℃, 298.15K, 10⁵Pa）においては以下のようになる。

また標準酸化還元電位との関係は以下の通りである。ここで n は価数、 F はファラデー定数である。

電池ではギブズエネルギー変化が負の値を取っている。

脚注

出典

関連項目

• 熱力学
• 化学ポテンシャル
• エクセルギー

UpToDate Contents

全文を閲覧するには購読必要です。 To read the full text you will need to subscribe.

• 1. 思春期における食物エネルギー所要量 dietary energy requirements in adolescents
• 2. 中等症から重症熱傷患者に対する栄養所要量および経腸栄養剤 nutritional demands and enteral formulas for moderate to severe burn patients
• 3. 肥満の病因 pathogenesis of obesity
• 4. 筋肉におけるエネルギー代謝 energy metabolism in muscle
• 5. HIV感染男性における性腺機能低下 hypogonadism in hiv infected males

Japanese Journal

• 誰でもわかる化学熱力学(7)エントロピーと自由エネルギー

• 中田 宗隆
• 現代化学 (489), 53-57, 2011-12
• NAID 40019072045

• QM/MM法と溶液の理論の融合による凝縮系の化学過程の自由エネルギー計算(13)凝縮系の第一原理計算の方法論について

• 高橋 英明
• アンサンブル : 分子シミュレーション研究会会誌 13(4), 157-160, 2011-10
• NAID 40019066732

Related Links

• 自由エネルギー：マピオン大百科

マピオン大百科へようこそ。このページは自由エネルギーに関する情報を掲載しています。気になる人物、知りたい事件があったらすぐに検索！ ... 自由エネルギー（じゆうエネルギー、英: free energy ）とは、熱力学における状態量の1つで ...

• 自由エネルギー - BIGLOBE百科事典

自由エネルギー（じゆうエネルギー、free energy）とは、熱力学における状態量の1つである。熱力学第一法則から導いた式によりエネルギーの収支を、第二法則から得た式によりある過程の進行の自発性を扱えるので、十分な物理量を得ると ...

Related Pictures

---

★リンクテーブル★

リンク元	「ピロリン酸」「Helmholtz free energy」
拡張検索	「標準自由エネルギー変化」「Gibbs自由エネルギー」
関連記事	「エネルギー」「自由」

「ピロリン酸」

　　[★]

英

pyrophosphate, PPi, pyrophosphoric acid

同

二リン酸 diphosphoric acid、焦性リン酸 pyrophosphoric acid、無機ピロリン酸 inorganic pyrophosphate

関

自由エネルギー

「Helmholtz free energy」

　　[★]

同

Helmholtz's free energy

関

自由エネルギー

「標準自由エネルギー変化」

　　[★]

■反応の速度 実際に標準自由エネルギーが負であるからといって、反応が自発的にどんどん進むことはなく、活性化エネルギーあるいは触媒の供給が必要である。

■平衡定数とΔGの関係 　物質Aの濃度と自由エネルギーの関係はほぼ次式で表される 　　GA - G゜A = RT [A] 　　　GA　：部分モル自由エネルギー、化学ポテンシャル 　　　G゜A：標準状態での部分モル自由エネルギー

　　aA + bB ⇔ cC + dD 　この反応の反応に伴う自由エネルギー変化ΔGは 　　ΔG 　= c * G　c + d * G　d - a * G　a - b * G　b 　標準状態では 　　ΔG゜ = c * G゜c + d * G゜d - a * G゜a - b * G゜b

                     [C]^c * [D]^d 

　ΔG = ΔG゜ + RT ln -------------

                     [A]^a * [B]^b 

　平衡状態では

                 [C]^c * [D]^d 

　ΔG゜ = - RT ln ------------- = - RT Keq

                 [A]^a * [B]^b 

　Keqは平衡定数なので

       [C]^c * [D]^d 

　Keq = ------------- = exp( -ΔG゜/RT )

       [A]^a * [B]^b 

　ΔG゜= - RT ln Keq //

英

standard free energy change

英

standard free energy

「Gibbs自由エネルギー」

　　[★]

英

Gibbs free energy

関

ギブズ自由エネルギー

「エネルギー」

　　[★]

英

energy

関

エネルギー代謝

• 食事のカロリー、熱量の意味で使われることがある。ちなみに肝硬変の代償期の食事は30-35cal/kgが推奨される。

「自由」

　　[★]

英

freedom、free、freely、ad libitum、(adv,abrv)ad lib

関

適宜、取り除く、無料、遊離、遊離型、含まない、フリー