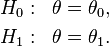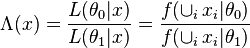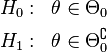Not to be confused with the use of likelihood ratios in diagnostic testing.
|
|
| This article has multiple issues. Please help improve it or discuss these issues on the talk page. |
|
|
This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. (September 2009) |
|
|
This article needs attention from an expert in Statistics. Please add a reason or a talk parameter to this template to explain the issue with the article. WikiProject Statistics (or its Portal) may be able to help recruit an expert. (November 2008) |
|
|
In statistics, a likelihood ratio test is a statistical test used to compare the goodness of fit of two models, one of which (the null model) is a special case of the other (the alternative model). The test is based on the likelihood ratio, which expresses how many times more likely the data are under one model than the other. This likelihood ratio, or equivalently its logarithm, can then be used to compute a p-value, or compared to a critical value to decide whether to reject the null model in favour of the alternative model. When the logarithm of the likelihood ratio is used, the statistic is known as a log-likelihood ratio statistic, and the probability distribution of this test statistic, assuming that the null model is true, can be approximated using Wilks's theorem.
In the case of distinguishing between two models, each of which has no unknown parameters, use of the likelihood ratio test can be justified by the Neyman–Pearson lemma, which demonstrates that such a test has the highest power among all competitors.
Contents
- 1 Use
- 2 Simple-vs-simple hypotheses
- 3 Definition (likelihood ratio test for composite hypotheses)
- 3.1 Interpretation
- 3.2 Distribution: Wilks's theorem
- 4 Examples
- 5 Notes
- 6 References
- 7 External links
Use
Each of the two competing models, the null model and the alternative model, is separately fitted to the data and the log-likelihood recorded. The test statistic (often denoted by D) is twice the log of the likelihoods ratio, i.e., it is twice the difference in the log-likelihoods:
![\begin{align}
D & = -2\ln\left( \frac{\text{likelihood for null model}}{\text{likelihood for alternative model}} \right) = 2\ln\left( \frac{\text{likelihood for alternative model}}{\text{likelihood for null model}} \right) \\
&= 2 \times [ \ln(\text{likelihood for alternative model}) - \ln(\text{likelihood for null model}) ] \\
\end{align}](//upload.wikimedia.org/math/0/3/d/03dceda06cfdd43c8becf8f28fc80b42.png)
The model with more parameters (here alternative) will always fit at least as well, i.e., have a greater or equal log-likelihood, than the model with less parameters (here null). Whether it fits significantly better and should thus be preferred is determined by deriving the probability or p-value of the difference D. Where the null hypothesis represents a special case of the alternative hypothesis, the probability distribution of the test statistic is approximately a chi-squared distribution with degrees of freedom equal to .[2] Symbols and represent the number of free parameters of models alternative and null, respectively.
Here is an example of use. If the null model has 1 parameter and a log-likelihood of −8024 and the alternative model has 3 parameters and a log-likelihood of −8012, then the probability of this difference is that of chi-squared value of with degrees of freedom, and is equal to . Certain assumptions must be met for the statistic to follow a chi-squared distribution, and often empirical p-values are computed.
The likelihood-ratio test requires nested models, i.e. models in which the more complex one can be transformed into the simpler model by imposing a set of constraints on the parameters. If the models are not nested, then a generalization of the likelihood-ratio test can usually be used instead: the relative likelihood.
Simple-vs-simple hypotheses
Main article: Neyman–Pearson lemma
A statistical model is often a parametrized family of probability density functions or probability mass functions . A simple-vs-simple hypothesis test has completely specified models under both the null and alternative hypotheses, which for convenience are written in terms of fixed values of a notional parameter :
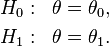
Note that under either hypothesis, the distribution of the data is fully specified; there are no unknown parameters to estimate. The likelihood ratio test is based on the likelihood ratio, which is often denoted by (the capital Greek letter lambda). The likelihood ratio is defined as follows:
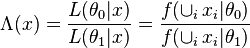
or
where is the likelihood function, and is the supremum function. Note that some references may use the reciprocal as the definition. In the form stated here, the likelihood ratio is small if the alternative model is better than the null model and the likelihood ratio test provides the decision rule as follows:
- If , do not reject ;
- If , reject ;
- Reject with probability if
The values are usually chosen to obtain a specified significance level , through the relation . The Neyman-Pearson lemma states that this likelihood ratio test is the most powerful among all level tests for this problem.
Definition (likelihood ratio test for composite hypotheses)
A null hypothesis is often stated by saying the parameter is in a specified subset of the parameter space .
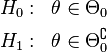
The likelihood function is (with being the pdf or pmf), which is a function of the parameter with held fixed at the value that was actually observed, i.e., the data. The likelihood ratio test statistic is
Here, the notation refers to the supremum function.
A likelihood ratio test is any test with critical region (or rejection region) of the form where is any number satisfying . Many common test statistics such as the Z-test, the F-test, Pearson's chi-squared test and the G-test are tests for nested models and can be phrased as log-likelihood ratios or approximations thereof.
Interpretation
Being a function of the data , the likelihood ratio is therefore a statistic. The likelihood ratio test rejects the null hypothesis if the value of this statistic is too small. How small is too small depends on the significance level of the test, i.e., on what probability of Type I error is considered tolerable ("Type I" errors consist of the rejection of a null hypothesis that is true).
The numerator corresponds to the maximum likelihood of an observed outcome under the null hypothesis. The denominator corresponds to the maximum likelihood of an observed outcome varying parameters over the whole parameter space. The numerator of this ratio is less than the denominator. The likelihood ratio hence is between 0 and 1. Low values of the likelihood ratio mean that the observed result was less likely to occur under the null hypothesis as compared to the alternative. High values of the statistic mean that the observed outcome was nearly as likely to occur under the null hypothesis as the alternative, and the null hypothesis cannot be rejected.
Distribution: Wilks's theorem
If the distribution of the likelihood ratio corresponding to a particular null and alternative hypothesis can be explicitly determined then it can directly be used to form decision regions (to accept/reject the null hypothesis). In most cases, however, the exact distribution of the likelihood ratio corresponding to specific hypotheses is very difficult to determine. A convenient result, attributed to Samuel S. Wilks, says that as the sample size approaches , the test statistic for a nested model will be asymptotically -distributed with degrees of freedom equal to the difference in dimensionality of and . This means that for a great variety of hypotheses, a practitioner can compute the likelihood ratio for the data and compare to the value corresponding to a desired statistical significance as an approximate statistical test.
Wilk's theorem assumes that the true but unknown values of the estimated parameters are in the interior of the parameter space. This is commonly violated in, for example, random or mixed effects models when one of the variance components is negligible relative to the others. In some such cases with one variance component essentially zero relative to the others or the models are not properly nested, Pinheiro and Bates showed that the true distribution of this likelihood ratio chi-square statistic could be substantially different from the naive , often dramatically so.[8] The naive assumptions could give significance probabilities (p-values) that are far too large on average in some cases and far too small in other.
In general, to test random effects, they recommend using Restricted maximum likelihood (REML). For fixed effects testing, they say, "a likelihood ratio test for REML fits is not feasible, because" changing the fixed effects specification changes the meaning of the mixed effects, and the restricted model is therefore not nested within the larger model.[9]
They simulated tests setting one and two random effects variances to zero. In those particular examples, the simulated p-values with k restrictions most closely matched a 50-50 mixture of and . (With k = 1, is 0 with probability 1. This means that a good approximation was .)
They also simulated tests of different fixed effects. In one test of a factor with 4 levels (degrees of freedom = 3), they found that a 50-50 mixture of and was a good match for actual p-values obtained by simulation -- and the error in using the naive "may not be too alarming.[10] However, in another test of a factor with 15 levels, they found a reasonable match to -- 4 more degrees of freedom than the 14 that one would get from a naive (inappropriate) application of Wilk's theorem, AND the simulated p-value was several times the naive . They conclude that for testing fixed effects, it's wise to use simulation. (And they provided a "simulate.lme" function in their "nlme" package for S-PLUS and R to support doing that.)
To be clear, these limitations on Wilk's theorem do not negate any power properties of a particular likelihood ratio test, only the use of a distribution to evaluate its statistical significance.
Examples
Coin tossing
An example, in the case of Pearson's test, we might try to compare two coins to determine whether they have the same probability of coming up heads. Our observation can be put into a contingency table with rows corresponding to the coin and columns corresponding to heads or tails. The elements of the contingency table will be the number of times the coin for that row came up heads or tails. The contents of this table are our observation .
|
Heads |
Tails |
| Coin 1 |
|
|
| Coin 2 |
|
|
Here consists of the possible combinations of values of the parameters , , , and , which are the probability that coins 1 and 2 come up heads or tails. In what follows, and . The hypothesis space is constrained by the usual constraints on a probability distribution, , and . The space of the null hypothesis is the subspace where . Writing for the best values for under the hypothesis , the maximum likelihood estimate is given by
Similarly, the maximum likelihood estimates of under the null hypothesis are given by
which does not depend on the coin .
The hypothesis and null hypothesis can be rewritten slightly so that they satisfy the constraints for the logarithm of the likelihood ratio to have the desired nice distribution. Since the constraint causes the two-dimensional to be reduced to the one-dimensional , the asymptotic distribution for the test will be , the distribution with one degree of freedom.
For the general contingency table, we can write the log-likelihood ratio statistic as
Notes
- ^ Huelsenbeck & Crandall 1997.
- ^ Pinheiro and Bates (2000)
- ^ Pinheiro and Bates (2000, p. 87)
- ^ Pinheiro and Bates (2000, p. 88)
References
- Casella, George; Berger, Roger L. (2001). Statistical Inference (Second ed.). ISBN 0-534-24312-6.
- Cox, D. R.; Hinkley, D. V. (1974). Theoretical Statistics. Chapman and Hall. ISBN 0-412-12420-3.
- Huelsenbeck, J. P.; Crandall, K. A. (1997). "Phylogeny Estimation and Hypothesis Testing Using Maximum Likelihood". Annual Review of Ecology and Systematics 28: 437–466. doi:10.1146/annurev.ecolsys.28.1.437.
- Mood, A.M.; Graybill, F.A. (1963). Introduction to the Theory of Statistics (2nd ed.). McGraw-Hill. ISBN 978-0070428638.
- Neyman, Jerzy; Pearson, Egon S. (1933). "On the Problem of the Most Efficient Tests of Statistical Hypotheses" (PDF). Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences 231 (694–706): 289–337. Bibcode:1933RSPTA.231..289N. doi:10.1098/rsta.1933.0009. JSTOR 91247.
- Pinheiro, José C.; Bates, Douglas M. (2000), Mixed-Effects Models in S and S-PLUS, Springer-Verlag, pp. 82–93, ISBN 0-387-98957-9
- Stuart, A.; Ord, K.; Arnold, S (1999). Kendall's Advanced Theory of Statistics 2A. Arnold.
- Wilks, S. S. (1938). "The Large-Sample Distribution of the Likelihood Ratio for Testing Composite Hypotheses". The Annals of Mathematical Statistics 9: 60–62. doi:10.1214/aoms/1177732360.
External links
- Practical application of likelihood ratio test described
- R Package: Wald's Sequential Probability Ratio Test
- Richard Lowry's Predictive Values and Likelihood Ratios Online Clinical Calculator








![\begin{align}
D & = -2\ln\left( \frac{\text{likelihood for null model}}{\text{likelihood for alternative model}} \right) = 2\ln\left( \frac{\text{likelihood for alternative model}}{\text{likelihood for null model}} \right) \\
&= 2 \times [ \ln(\text{likelihood for alternative model}) - \ln(\text{likelihood for null model}) ] \\
\end{align}](http://upload.wikimedia.org/math/0/3/d/03dceda06cfdd43c8becf8f28fc80b42.png)