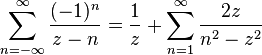三角関数(さんかくかんすう、英: trigonometric function)とは、平面三角法において直角三角形の角の大きさから辺の比を与える関数の族および、それらを拡張して得られる関数の総称である。
|
目次
- 1 定義
- 1.1 直角三角形における定義
- 1.2 単位円における定義
- 2 歴史
- 3 三角関数の性質
- 3.1 周期性
- 3.2 相互関係
- 3.3 加法定理
- 4 微積分
- 5 級数展開
- 6 無限乗積展開
- 7 部分分数展開
- 8 逆三角関数
- 9 複素関数への拡張
- 10 球面三角法
- 11 関連項目
- 12 外部リンク
|
定義
直角三角形における定義
直角三角形は1つの角が直角であり、三角形の内角の和は180度であることから他の1つの角の大きさが定まれば、角の大きさが3つとも決まり三角形の3辺の比も決まる。ゆえに角の大きさを与えることで、辺同士の比を返すような関数を考えることができる。
∠C を直角とする直角三角形 △ABC において ∠A = θ を与えれば、 3辺の比 AB : BC : CA が定まることから、h = AB, a = BC, b = CA とおくと、
という6つの値が定まる。それぞれ正弦(サイン/sine)・余弦(コサイン/cosine)・正接(タンジェント/tangent)・余割(コセカント/cosecant)・正割(セカント/secant)・余接(コタンジェント/cotangent)と呼ばれ、まとめて三角比と呼ばれる。余弦とは、余りの角、すなわちその角と直角以外の角の正弦を意味する。三角比は平面三角法に用いられ、巨大なものの大きさや遠方までの距離を計算する際の便利な道具となる。角度 θ の単位は普通、度かラジアンである。
単位円における定義
点Oを中心とする単位円上での全ての三角関数の定義。
2次元ユークリッド空間 R2 における単位円 x2 + y2 = 1 上で、点 (1,0) から正の向きに回転する動点 P = (x,y) に対して、動点と原点を結ぶ線分が x 軸の正方向と成す角を t として、
と定義する(ただし、tは反時計回りの向きを正として測る)。上から正弦関数(sine; サイン)・余弦関数(cosine; コサイン)・正接関数(tangent; タンジェント)と呼び、これらを総称して三角関数と呼ぶ。さらにその逆数、
を、上から余割関数(cosecant; コセカント)・正割関数(secant; セカント)・余接関数(cotangent; コタンジェント)と呼び、これらを総称して割三角関数(かつさんかくかんすう)と呼ぶ。また、割三角関数を含めて三角関数と呼ぶこともある。cosec は長いため、主に csc と書く。
歴史
一定の半径の円における中心角に対する弦と弧の長さの関係は、測量や天文学の要請によって古代から研究されてきた。
古代ギリシャにおいて、円と球に基づく宇宙観に則った天文学研究から、ヒッパルコスにより一定の半径の円における中心角に対する弦の長さが表にまとめられたもの(正弦表)が作られた。プトレマイオスの『アルマゲスト』にも正弦表が記載されている。
正弦表は後にインドに伝わり、弦の長さは半分でよいという考えから5世紀ごろには半弦 ardha-jiva (つまり現在の sine の意味の正弦)の長さをより精確にまとめたものが作成された(『アールヤバタ』)。ardha は"半分" jiva は"弦"の意味で、当時のインドではこの半弦(現在の sine の意味の正弦)は単に jiva と略された。また、弦の長さを半分にして直角三角形を当てはめたことから派生して余角 (complementary angle) の考えが生まれ、“余角 (co-angle) の正弦 (sine)”という考えから余弦 (cosine) の考えが生まれた。余弦の値もこのころに詳しく調べられている。
(*co- は complementary の略で、補完的・補足的という意味の接頭語として用いる)
8世紀ごろアラビアへ伝わったときに jaib(入り江)と変化して、一説では12世紀にチェスターのロバートがラテン語に翻訳した際、正弦を sinus rectus と意訳し(sinusはラテン語で「湾」のこと)、現在の sine になったという。
また、10世紀の数学者アル・バッターニが正弦法の導入、コタンジェント表の計算、球面三角法(球面幾何学)の定理を提唱した。
円や弦といった概念からは独立に、三角比を辺の比として角と長さの関係と捉えたのは16世紀ドイツのラエティクスであると言われる。余弦を co-sine とよんだり、sin, cos という記号が使われるようになったりしたのは 17世紀になってからであり、それが定着するのは 18世紀オイラーのころである。一般角に対する三角関数を定義したのはオイラーである。
三角関数の性質
周期性
sin
x と cos
x のグラフ。周期性が確認できる
単位円上を往く動点 P は 2π の行程を隔てれば、単位円を一周する。従って、任意の行程 t は、
と表現することができる。この時、θ を偏角、t を一般角と言う。偏角でも一般角でも、最終到達点の座標は一致するわけであるから、
が成り立つ(他の三角関数でも同様)。このことから、三角関数は周期関数となる。
相互関係
詳細は「三角関数の公式の一覧」を参照
単位円上の動点の座標によって定まる関数であることから、三角関数の間には多数の相互関係が存在する。
- 基本相互関係
- 全てピタゴラスの定理により証明される。
- 負角・余角・補角公式
-
加法定理
加法定理の導出
ここでは例としてオイラーの公式を用いた導出を記す。
オイラーの公式から、
として実部と虚部を比較すると sin, cos の加法公式を得る。また、
において分母と分子を で割ると tan の加法公式が得られる。
なお、当然のことながら、ここで述べた導出法はオイラーの公式を既知とするように三角関数の導入(たとえば三角関数をべき級数として定義)を行っていなければ通用しない。
微積分
三角関数の微積分は、以下の表の通りである。
-
三角関数の微分では、次の極限
の成立が基本的である。このとき、sin x の導関数が cos x であることは加法定理から従う。さらに余角公式 cos x = sin(x + π/2) から cos x の導関数は sin(x + π) = −sin x である。即ち、sin x は微分方程式の特殊解である。また、他の三角関数の導関数も、上の事実から簡単に導ける。
級数展開
三角関数は以下のようにテイラー級数に展開される。解析学では、幾何的な性質へ言及せず、これらの表示を三角関数の定義とすることがある。z は任意の複素数である。Bn は、ベルヌーイ数である。En は オイラー数である。
無限乗積展開
三角関数は以下のように無限乗積に展開される。(→証明)
部分分数展開
三角関数は以下のように部分分数に展開される。(→証明)
逆三角関数
三角関数の定義域を適当に制限したものの逆関数を逆三角関数(ぎゃくさんかくかんすう、inverse trigonometric function)とよぶ。逆三角関数は逆関数の記法に則り、元の関数の記号に −1 を右肩に付して表す。たとえば逆正弦関数(ぎゃくせいげんかんすう、inverse sine; インバース・サイン)は sin−1 x などと表す。arcsin, arccos などの記法もよく用いられる。
である。逆関数は逆数ではないので注意したい。逆数との混乱を避けるために、逆正弦関数 sin−1 x を arcsin x と書く流儀もある。一般に周期関数の逆関数は多価関数になるので、通常は逆三角関数を一価連続なる枝に制限して考えることが多い。たとえば、便宜的に主値と呼ばれる枝を
のように選ぶことが多い。またこのとき、制限があることを強調するために、Sin−1 x, Arcsin x のように頭文字を大文字にした表記がよく用いられる。
複素関数への拡張
三角関数の微分に関する性質から、cos x, sin x をテイラー展開することにより、かの有名なオイラーの公式 exp(ix) = cos x + isin x が導かれる。これより、2つの等式、
exp(ix) = cos x + i sin x
exp(−ix) = cos x − i sin x
が得られるから、これを連立させて解くことにより、正弦関数・余弦関数の初等関数としての表現が可能となる。即ち、
この事実を用いて三角関数の定義域を複素数全体に拡張することができる。まず、
である。ここで cosh x , sinh x は双曲線関数を指す。この等式は三角関数と双曲線関数の関係式と捉えることもできる。任意の複素数 z は z = x+iy (x,y∈R) と表現できるから、加法定理より
cos z = cos(x+iy) = cos x cosh y − i sin x sinh y,
sin z = sin(x+iy) = sin x cosh y + i cos x sinh y
が成り立つ。これこそが正弦関数・余弦関数の定義域を複素数全体に拡張した物である。他の三角関数も正弦関数と余弦関数の四則演算によって定義できるから、結局全ての三角関数は定義域を複素数全体に拡張できることがわかる。
球面三角法
球面の三角形 ABCの内角を a,b,c, 各頂点の対辺に関する球の中心角をα,β,γとするとき、次のような関係が成立する。余弦公式や正弦余弦公式は式の対称性により各記号を入れ替えたものも成立する。
- 正弦公式: sin a : sin b : sin c = sin α : sin β : sin γ
- 余弦公式: cos a = - cos b cos c + sin b sin c cos α
- 余弦公式: cos α = cos β cos γ + sin β sin γ cos a
- 正弦余弦公式: sin a cos β = cos b sin c − sin b cos c cos α
関連項目
- 正弦定理
- 余弦定理
- 正接定理
- 球面三角法
- コサイン4乗則
外部リンク
- Weisstein, Eric W., "Trigonometric Functions" - MathWorld.(英語)
- 三角比の近似値表
For other uses, see Sine (disambiguation).
|
Sine
|
|
|
| Basic features |
| Parity |
odd |
| Domain |
(−∞,∞) |
| Codomain |
[−1,1] |
| Period |
2π |
| Specific values |
| At zero |
0 |
| Maxima |
((2k + ½)π, 1) |
| Minima |
((2k − ½)π, −1) |
| Specific features |
| Root |
kπ |
| Critical point |
kπ − π/2 |
| Inflection point |
kπ |
| Fixed point |
0 |
| Variable k is an integer. Domain and codomain are given only for real (not complex) numbers. |
For the angle α, the sine function gives the ratio of the length of the opposite side to the length of the hypotenuse.
The sine function graphed on the Cartesian plane. In this graph, the angle
x is given in radians (π = 180°).
The sine and cosine functions are related in multiple ways. The derivative of is . Also they are out of phase by 90°: = . And for a given angle, cos and sin give the respective x, y coordinates on a unit circle.
In mathematics, the sine function is a function of an angle. In a right triangle, sine gives the ratio of the length of the side opposite to an angle to the length of the hypotenuse.
Sine is usually listed first amongst the trigonometric functions.
Trigonometric functions are commonly defined as ratios of two sides of a right triangle containing the angle, and can equivalently be defined as the lengths of various line segments from a unit circle. More modern definitions express them as infinite series or as solutions of certain differential equations, allowing their extension to arbitrary positive and negative values and even to complex numbers.
The sine function is commonly used to model periodic phenomena such as sound and light waves, the position and velocity of harmonic oscillators, sunlight intensity and day length, and average temperature variations throughout the year.
The function sine can be traced to the jyā and koṭi-jyā functions used in Gupta period Indian astronomy (Aryabhatiya, Surya Siddhanta), via translation from Sanskrit to Arabic and then from Arabic to Latin.[1] The word "sine" comes from a Latin mistranslation of the Arabic jiba, which is a transliteration of the Sanskrit word for half the chord, jya-ardha.[2]
|
Contents
- 1 Right-angled triangle definition
- 2 Relation to slope
- 3 Relation to the unit circle
- 4 Identities
- 4.1 Reciprocal
- 4.2 Inverse
- 4.3 Calculus
- 4.4 Other trigonometric functions
- 5 Properties relating to the quadrants
- 6 Series definition
- 7 Continued fraction
- 8 Fixed point
- 9 Law of sines
- 10 Values
- 11 Relationship to complex numbers
- 11.1 Sine with a complex argument
- 11.1.1 Partial fraction and product expansions of complex sine
- 11.1.2 Usage of complex sine
- 11.2 Complex graphs
- 12 History
- 13 Software implementations
- 14 See also
- 15 Notes
|
Right-angled triangle definition
For any similar triangle the ratio of the length of the sides remains the same. For example, if the hypotenuse is twice as long, so are the other sides. Therefore respective trigonometric functions, depending only on the size of the angle, express those ratios: between the hypotenuse and the "opposite" side to an angle A in question (see illustration) in the case of sine function; or between the hypotenuse and the "adjacent" side (cosine) or between the "opposite" and the "adjacent" side (tangent), etc.
To define the trigonometric functions for an acute angle A, start with any right triangle that contains the angle A. The three sides of the triangle are named as follows:
- The hypotenuse is the side opposite the right angle, in this case side h. The hypotenuse is always the longest side of a right-angled triangle.
- The opposite side is the side opposite to the angle we are interested in (angle A), in this case side a.
- The adjacent side is the side that is in contact with (adjacent to) both the angle we are interested in (angle A) and the right angle, in this case side b.
In ordinary Euclidean geometry, according to the triangle postulate the inside angles of every triangle total 180° (π radians). Therefore, in a right-angled triangle, the two non-right angles total 90° (π/2 radians), so each of these angles must be greater than 0° and less than 90°. The following definition applies to such angles.
The angle A (having measure α) is the angle between the hypotenuse and the adjacent line.
The sine of an angle is the ratio of the length of the opposite side to the length of the hypotenuse. In our case
Note that this ratio does not depend on the size of the particular right triangle chosen, as long as it contains the angle A, since all such triangles are similar.
Relation to slope
Main article: Slope
The trigonometric functions can be defined in terms of the rise, run, and slope of a line segment relative to some horizontal line.
- When the length of the line segment is 1, sine takes an angle and tells the rise
- Sine takes an angle and tells the rise per unit length of the line segment.
- Rise is equal to sin θ multiplied by the length of the line segment
In contrast, cosine is used for the telling the run from the angle; and tangent is used for telling the slope from the angle. Arctan is used for telling the angle from the slope.
The line segment is the equivalent of the hypotenuse in the right-triangle, and when it has a length of 1 it is also equivalent to the radius of the unit circle.
Relation to the unit circle
In trigonometry, a unit circle is the circle of radius one centered at the origin (0, 0) in the Cartesian coordinate system.
Let a line through the origin, making an angle of θ with the positive half of the x-axis, intersect the unit circle. The x- and y-coordinates of this point of intersection are equal to cos θ and sin θ, respectively. The point's distance from the origin is always 1.
Unlike the definitions with the right or left triangle or slope, the angle can be extended to the full set of real arguments by using the unit circle. This can also be achieved by requiring certain symmetries and that sine be a periodic function.
|
|
Illustration of a unit circle. The radius has a length of 1. The variable t is an angle measure.
|
Point P( x, y) on the circle of unit radius at an obtuse angle θ > π/2
|
Animation showing the graphing process of y = sin x (where x is the angle in radians) using a unit circle. The blue arc around the unit circle (in green) and the blue line at right have the same length, equal to the angle in radians.
Identities
See also: List of trigonometric identities
Exact identities (using radians):
These apply for all values of .
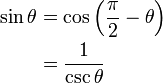
Reciprocal
The reciprocal of sine is cosecant, i.e. the reciprocal of sin(A) is csc(A), or cosec(A). Cosecant gives the ratio of the length of the hypotenuse to the length of the opposite side:
Inverse
The usual principal values of the arcsin(x) function graphed on the cartesian plane. Arcsin is the inverse of sin.
The inverse function of sine is arcsine (arcsin or asin) or inverse sine (sin−1). As sine is non-injective, it is not an exact inverse function but a partial inverse function. For example, sin(0) = 0, but also sin(π) = 0, sin(2π) = 0 etc. It follows that the arcsine function is multivalued: arcsin(0) = 0, but also arcsin(0) = π, arcsin(0) = 2π, etc. When only one value is desired, the function may be restricted to its principal branch. With this restriction, for each x in the domain the expression arcsin(x) will evaluate only to a single value, called its principal value.
k is some integer:

Or in one equation:
Arcsin satisfies:
and
Calculus
See also: List of integrals of trigonometric functions and Differentiation of trigonometric functions
For the sine function:
The derivative is:
The antiderivative is:
C denotes the constant of integration.
Other trigonometric functions
The four quadrants of a Cartesian coordinate system.
It is possible to express any trigonometric function in terms of any other (up to a plus or minus sign, or using the sign function).
Sine in terms of the other common trigonometric functions:
|
f θ |
Using plus/minus (±) |
Using sign function (sgn) |
| f θ = |
± per Quadrant |
f θ = |
| I |
II |
III |
IV |
| cos |
|
|
+ |
+ |
- |
- |
|
|
|
+ |
- |
- |
+ |
|
| cot |
|
|
+ |
+ |
- |
- |
|
|
|
+ |
- |
- |
+ |
|
| tan |
|
|
+ |
- |
- |
+ |
|
|
|
+ |
- |
- |
+ |
|
| sec |
|
|
+ |
- |
+ |
- |
|
|
|
+ |
- |
- |
+ |
|
Note that for all equations which use plus/minus (±), the result is positive for angles in the first quadrant.
The basic relationship between the sine and the cosine can also be expressed as the Pythagorean trigonometric identity:
where sin2x means (sin(x))2.
Properties relating to the quadrants
Over the four quadrants of the sine function is as follows.
| Quadrant |
Degrees |
Radians |
Value |
Sign |
Monotony |
Convexity |
| 1st Quadrant |
|
|
|
|
increasing |
concave |
| 2nd Quadrant |
|
|
|
|
decreasing |
concave |
| 3rd Quadrant |
|
|
|
|
decreasing |
convex |
| 4th Quadrant |
|
|
|
|
increasing |
convex |
Points between the quadrants. k is an integer.
The quadrants of the unit circle and of
sin x, using the Cartesian coordinate system.
| Degrees |
Radians
0 ≤ x < 2π
|
Radians |
sin x |
Point type |
| 0° |
0 |
|
0 |
Root, Inflection |
| 90° |
|
|
1 |
Maxima |
| 180° |
|
|
0 |
Root, Inflection |
| 270° |
|
|
-1 |
Minima |
For arguments outside those in the table, get the value using the fact the sine function has a period of 360° (or 2π rad): , or use . Or use and For complement of sine, we have
Series definition
The sine function (blue) is closely approximated by its Taylor polynomial of degree 7 (pink) for a full cycle centered on the origin.
This animation shows how including more and more terms in the partial sum of its Taylor series gradually builds up a sine curve.
Using only geometry and properties of limits, it can be shown that the derivative of sine is cosine, and that the derivative of cosine is the negative of sine.
Using the reflection from the calculated geometric derivation of the sine is with the 4n + k-th derivative at the point 0:

This gives the following Taylor series expansion at x = 0. One can then use the theory of Taylor series to show that the following identities hold for all real numbers x (where x is the angle in radians) :[3]
![\begin{align}
\sin x & = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \cdots \\[8pt]
& = \sum_{n=0}^\infty \frac{(-1)^n}{(2n+1)!}x^{2n+1} \\[8pt]
\end{align}](//upload.wikimedia.org/math/3/4/b/34b34cb6687b3991cbf0b36eaa279739.png)
If x were expressed in degrees then the series would contain messy factors involving powers of π/180: if x is the number of degrees, the number of radians is y = πx /180, so

The series formulas for the sine and cosine are uniquely determined, up to the choice of unit for angles, by the requirements that

The radian is the unit that leads to the expansion with leading coefficient 1 for the sine and is determined by the additional requirement that

The coefficients for both the sine and cosine series may therefore be derived by substituting their expansions into the pythagorean and double angle identities, taking the leading coefficient for the sine to be 1, and matching the remaining coefficients.
In general, mathematically important relationships between the sine and cosine functions and the exponential function (see, for example, Euler's formula) are substantially simplified when angles are expressed in radians, rather than in degrees, grads or other units. Therefore, in most branches of mathematics beyond practical geometry, angles are generally assumed to be expressed in radians.
A similar series is Gregory's series for arctan, which is obtained by omitting the factorials in the denominator.
Continued fraction
The sine function can also be represented as a generalized continued fraction:

The continued fraction representation expresses the real number values, both rational and irrational, of the sine function.
Fixed point
The fixed point iteration
xn+1 = sin
xn with initial value
x0 = 2 converges to 0.
Zero is the only real fixed point of the sine function; in other words the only intersection of the sine function and the identity function is sin(0) = 0.
Law of sines
Main article: Law of sines
The law of sines states that for an arbitrary triangle with sides a, b, and c and angles opposite those sides A, B and C:
This is equivalent to the equality of the first three expressions below:
where R is the triangle's circumradius.
It can be proven by dividing the triangle into two right ones and using the above definition of sine. The law of sines is useful for computing the lengths of the unknown sides in a triangle if two angles and one side are known. This is a common situation occurring in triangulation, a technique to determine unknown distances by measuring two angles and an accessible enclosed distance.
Values
See also: Exact trigonometric constants
Some common angles (
θ) shown on the unit circle. The angles are given in degrees and radians, together with the corresponding intersection point on the unit circle, (cos
θ, sin
θ).
| x (angle) |
sin x |
| Degrees |
Radians |
Grads |
Exact |
Decimal |
| 0° |
0 |
0g |
0 |
0 |
| 180° |
|
200g |
| 15° |
|
162⁄3g |
|
0.258819045102521 |
| 165° |
|
1831⁄3g |
| 30° |
|
331⁄3g |
|
0.5 |
| 150° |
|
1662⁄3g |
| 45° |
|
50g |
|
0.707106781186548 |
| 135° |
|
150g |
| 60° |
|
662⁄3g |
|
0.866025403784439 |
| 120° |
|
1331⁄3g |
| 75° |
|
831⁄3g |
|
0.965925826289068 |
| 105° |
|
1162⁄3g |
| 90° |
|
100g |
1 |
1 |
A memory aid (note it does not include 15° and 75°):
| x in degrees |
0° |
30° |
45° |
60° |
90° |
| x in radians |
0 |
π/6 |
π/4 |
π/3 |
π/2 |
|
|
|
|
|
|
90 degree increments:
| x in degrees |
0° |
90° |
180° |
270° |
360° |
| x in radians |
0 |
π/2 |
π |
3π/2 |
2π |
|
0 |
1 |
0 |
-1 |
0 |
Other values not listed above:
- A019812
- A019815
- A019818
- A019821
- A019827
- A019830
- A019833
- A019836
- A019842
- A019845
- A019848
- A019851
For angles greater than 2π or less than −2π, simply continue to rotate around the circle; sine periodic function with period 2π:
for any angle θ and any integer k.
The primitive period (the smallest positive period) of sine is a full circle, i.e. 2π radians or 360 degrees.
Relationship to complex numbers
Main article: Trigonometric functions#Relationship to exponential function and complex numbers
An illustration of the complex plane. The imaginary numbers are on the vertical coordinate axis.
Sine is used to determine the imaginary part of a complex number given in polar coordinates (r,φ):
the imaginary part is:
r and φ represent the magnitude and angle of the complex number respectively. i is the imaginary unit. z is a complex number.
Although dealing with complex numbers, sine's parameter in this usage is still a real number. Sine can also take a complex number as an argument.
Sine with a complex argument
Domain coloring of sin(z) over (-π,π) on x and y axes. Brightness indicates absolute magnitude, saturation represents imaginary and real magnitude.
The definition of the sine function for complex arguments z:

where i 2 = −1. This is an entire function. Also, for purely real x,
For purely imaginary numbers:
It is also sometimes useful to express the complex sine function in terms of the real and imaginary parts of its argument:

Partial fraction and product expansions of complex sine
Using the partial fraction expansion technique in Complex Analysis, one can find that the infinite series
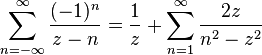
both converge and are equal to .
Similarly we can find

Using product expansion technique, one can derive

Usage of complex sine
sin z is found in the functional equation for the Gamma function,
- .
Which in turn is found in the functional equation for the Riemann zeta-function,
As a holomorphic function, sin z is a 2D solution of Laplace's equation:
Complex graphs
Sine function in the complex plane
|
|
|
|
| real component |
imaginary component |
magnitude |
Arcsine function in the complex plane
|
|
|
|
| real component |
imaginary component |
magnitude |
History
Main article: History of trigonometric functions
While the early study of trigonometry can be traced to antiquity, the trigonometric functions as they are in use today were developed in the medieval period. The chord function was discovered by Hipparchus of Nicaea (180–125 BC) and Ptolemy of Roman Egypt (90–165 AD).
The function sine (and cosine) can be traced to the jyā and koṭi-jyā functions used in Gupta period Indian astronomy (Aryabhatiya, Surya Siddhanta), via translation from Sanskrit to Arabic and then from Arabic to Latin.[1]
The first published use of the abbreviations 'sin', 'cos', and 'tan' is by the 16th century French mathematician Albert Girard; these were further promulgated by Euler (see below). The Opus palatinum de triangulis of Georg Joachim Rheticus, a student of Copernicus, was probably the first in Europe to define trigonometric functions directly in terms of right triangles instead of circles, with tables for all six trigonometric functions; this work was finished by Rheticus' student Valentin Otho in 1596.
In a paper published in 1682, Leibniz proved that sin x is not an algebraic function of x.[4] Roger Cotes computed the derivative of sine in his Harmonia Mensurarum (1722).[5] Leonhard Euler's Introductio in analysin infinitorum (1748) was mostly responsible for establishing the analytic treatment of trigonometric functions in Europe, also defining them as infinite series and presenting "Euler's formula", as well as the near-modern abbreviations sin., cos., tang., cot., sec., and cosec.[6]
Etymology
Etymologically, the word sine derives from the Sanskrit word for chord, jiva*(jya being its more popular synonym). This was transliterated in Arabic as jiba جــيــب, abbreviated jb جــــب . Since Arabic is written without short vowels, "jb" was interpreted as the word jaib جــيــب, which means "bosom", when the Arabic text was translated in the 12th century into Latin by Gerard of Cremona. The translator used the Latin equivalent for "bosom", sinus (which means "bosom" or "bay" or "fold") [7][8] The English form sine was introduced in the 1590s.
Software implementations
See also: Lookup table#Computing sines
The sin function, along with other trigonometric functions, is widely available across programming languages and platforms. Some CPU architectures have a built-in instruction for sin, including the Intel x87 FPU. In programming languages, sin is usually either a built in function or found within the language's standard math library.
There is no standard algorithm for calculating sin. IEEE 754-2008, the most widely used standard for floating-point computation, says nothing on the topic of calculating trigonometric functions such as sin.[9] Algorithms for calculating sin may be balanced for such constraints as speed, accuracy, portability, or range of input values accepted. This can lead to very different results for different algorithms in special circumstances, such as for very large inputs, e.g. sin(1022).
A once common programming optimization, used especially in 3D graphics, was to pre-calculate a table of sin values, for example a value per degree. This allowed results to be looked up from a table rather than being calculated in real time. With modern CPU architectures this method typically offers no advantage.[citation needed]
See also
| Trigonometry |
History
Usage
Functions
Generalized
Inverse functions
Further reading |
| Reference |
Identities
Exact constants
Trigonometric tables |
| Laws and theorems |
Law of sines
Law of cosines
Law of tangents
Law of cotangents
Pythagorean theorem |
| Calculus |
Trigonometric substitution
Integrals of functions
Derivatives of functions
Integrals of inverse functions |
|
|
- Sine wave
- Trigonometric functions
- Sinusoidal model
- Discrete sine transform
- Law of sines
- Sine and cosine transforms
- Sine quadrant
- Aryabhata's sine table
- Madhava's sine table
- Madhava series
- Bhaskara I's sine approximation formula
- Hyperbolic function
- List of trigonometric identities
- Proofs of trigonometric identities
- Euler's formula
- Polar sine — a generalization to vertex angles
- Optical sine theorem
- Generalized trigonometry
- Sine–Gordon equation
Notes
- ^ a b Boyer, Carl B. (1991). A History of Mathematics (Second ed.). John Wiley & Sons, Inc.. ISBN 0-471-54397-7, p. 210.
- ^ Victor J Katx, A history of mathematics, p210, sidebar 6.1.
- ^ See Ahlfors, pages 43–44.
- ^ Nicolás Bourbaki (1994). Elements of the History of Mathematics. Springer.
- ^ "Why the sine has a simple derivative", in Historical Notes for Calculus Teachers by V. Frederick Rickey
- ^ See Boyer (1991).
- ^ See Maor (1998), chapter 3, regarding the etymology.
- ^ Victor J Katx, A history of mathematics, p210, sidebar 6.1.
- ^ Grand Challenges of Informatics, Paul Zimmermann. September 20, 2006 – p. 14/31 [1]








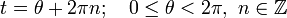










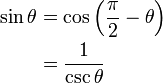


![\begin{align}
\sin x & = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \cdots \\[8pt]
& = \sum_{n=0}^\infty \frac{(-1)^n}{(2n+1)!}x^{2n+1} \\[8pt]
\end{align}](http://upload.wikimedia.org/math/3/4/b/34b34cb6687b3991cbf0b36eaa279739.png)