WordNet
- the trace of a point whose direction of motion changes (同)curved shape
- a pitch of a baseball that is thrown with spin so that its path curves as it approaches the batter (同)curve ball, breaking ball, bender
- a line on a graph representing data
- the 18th letter of the Roman alphabet (同)r
- an inferior dog or one of mixed breed (同)mongrel, mutt
- a cowardly and despicable person
- mythical bird of prey having enormous size and strength
- having or marked by a curve or smoothly rounded bend; "the curved tusks of a walrus"; "his curved lips suggested a smile but his eyes were hard" (同)curving
PrepTutorEJDIC
- 『曲線』 / 『曲がり』,曲がったもの,湾曲部 / (野球で投球の)『カーブ』 / (…の方へ)『曲がる』,湾曲する《+『to』+『名』》 / …'を'曲げる;'を'湾曲させる
- resistance / 17歳以下父兄同伴映画の表示 / rook
- のら犬 / くだらない人間
- ロック(アラビア神話の巨大な怪鳥でひな鳥を育てるのに象をえさにしたという)
Wikipedia preview
出典(authority):フリー百科事典『ウィキペディア(Wikipedia)』「2015/07/07 18:19:59」(JST)
wiki en
In statistics, a receiver operating characteristic (ROC), or ROC curve, is a graphical plot that illustrates the performance of a binary classifier system as its discrimination threshold is varied. The curve is created by plotting the true positive rate against the false positive rate at various threshold settings. The true-positive rate is also known as sensitivity or the sensitivity index d', known as "d-prime" in signal detection and biomedical informatics, or recall in machine learning. The false-positive rate is also known as the fall-out and can be calculated as 1 - specificity. The ROC curve is thus the sensitivity as a function of fall-out. In general, if the probability distributions for both detection and false alarm are known, the ROC curve can be generated by plotting the cumulative distribution function (area under the probability distribution from to ) of the detection probability in the y-axis versus the cumulative distribution function of the false-alarm probability in x-axis.
ROC analysis provides tools to select possibly optimal models and to discard suboptimal ones independently from (and prior to specifying) the cost context or the class distribution. ROC analysis is related in a direct and natural way to cost/benefit analysis of diagnostic decision making.
The ROC curve was first developed by electrical engineers and radar engineers during World War II for detecting enemy objects in battlefields and was soon introduced to psychology to account for perceptual detection of stimuli. ROC analysis since then has been used in medicine, radiology, biometrics, and other areas for many decades and is increasingly used in machine learning and data mining research.
The ROC is also known as a relative operating characteristic curve, because it is a comparison of two operating characteristics (TPR and FPR) as the criterion changes.[1]
Contents
- 1 Basic concept
- 2 ROC space
- 3 Curves in ROC space
- 4 Further interpretations
- 4.1 Area under the curve
- 4.2 Other measures
- 5 Detection error tradeoff graph
- 6 Z-score
- 7 History
- 8 ROC curves beyond binary classification
- 9 See also
- 10 References
- 10.1 General references
- 11 Further reading
- 12 External links
Basic concept
A classification model (classifier or diagnosis) is a mapping of instances between certain classes/groups. The classifier or diagnosis result can be a real value (continuous output), in which case the classifier boundary between classes must be determined by a threshold value (for instance, to determine whether a person has hypertension based on a blood pressure measure). Or it can be a discrete class label, indicating one of the classes.
Let us consider a two-class prediction problem (binary classification), in which the outcomes are labeled either as positive (p) or negative (n). There are four possible outcomes from a binary classifier. If the outcome from a prediction is p and the actual value is also p, then it is called a true positive (TP); however if the actual value is n then it is said to be a false positive (FP). Conversely, a true negative (TN) has occurred when both the prediction outcome and the actual value are n, and false negative (FN) is when the prediction outcome is n while the actual value is p.
To get an appropriate example in a real-world problem, consider a diagnostic test that seeks to determine whether a person has a certain disease. A false positive in this case occurs when the person tests positive, but actually does not have the disease. A false negative, on the other hand, occurs when the person tests negative, suggesting they are healthy, when they actually do have the disease.
Let us define an experiment from P positive instances and N negative instances for some condition. The four outcomes can be formulated in a 2×2 contingency table or confusion matrix, as follows:
| Condition (as determined by "Gold standard") | |||||
| Total population | Condition positive | Condition negative | Prevalence = Σ Condition positive/Σ Total population | ||
| Test outcome |
Test outcome positive |
True positive | False positive (Type I error) |
Positive predictive value (PPV), Precision = Σ True positive/Σ Test outcome positive | False discovery rate (FDR) = Σ False positive/Σ Test outcome positive |
| Test outcome negative |
False negative (Type II error) |
True negative | False omission rate (FOR) = Σ False negative/Σ Test outcome negative | Negative predictive value (NPV) = Σ True negative/Σ Test outcome negative | |
| Accuracy (ACC) = Σ True positive + Σ True negative/Σ Total population | True positive rate (TPR), Sensitivity, Recall = Σ True positive/Σ Condition positive | False positive rate (FPR), Fall-out = Σ False positive/Σ Condition negative | Positive likelihood ratio (LR+) = TPR/FPR | Diagnostic odds ratio (DOR) = LR+/LR− | |
| False negative rate (FNR), Miss rate = Σ False negative/Σ Condition positive | True negative rate (TNR), Specificity (SPC) = Σ True negative/Σ Condition negative | Negative likelihood ratio (LR−) = FNR/TNR | |||
ROC space
The contingency table can derive several evaluation "metrics" (see infobox). To draw a ROC curve, only the true positive rate (TPR) and false positive rate (FPR) are needed (as functions of some classifier parameter). The TPR defines how many correct positive results occur among all positive samples available during the test. FPR, on the other hand, defines how many incorrect positive results occur among all negative samples available during the test.
A ROC space is defined by FPR and TPR as x and y axes respectively, which depicts relative trade-offs between true positive (benefits) and false positive (costs). Since TPR is equivalent to sensitivity and FPR is equal to 1 − specificity, the ROC graph is sometimes called the sensitivity vs (1 − specificity) plot. Each prediction result or instance of a confusion matrix represents one point in the ROC space.
The best possible prediction method would yield a point in the upper left corner or coordinate (0,1) of the ROC space, representing 100% sensitivity (no false negatives) and 100% specificity (no false positives). The (0,1) point is also called a perfect classification. A completely random guess would give a point along a diagonal line (the so-called line of no-discrimination) from the left bottom to the top right corners (regardless of the positive and negative base rates). An intuitive example of random guessing is a decision by flipping coins (heads or tails). As the size of the sample increases, a random classifier's ROC point migrates towards (0.5,0.5).
The diagonal divides the ROC space. Points above the diagonal represent good classification results (better than random), points below the line poor results (worse than random). Note that the output of a consistently poor predictor could simply be inverted to obtain a good predictor.
Let us look into four prediction results from 100 positive and 100 negative instances:
| A | B | C | C′ | ||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
|
|
||||||||||||||||||||||||||||||||||||
| TPR = 0.63 | TPR = 0.77 | TPR = 0.24 | TPR = 0.76 | ||||||||||||||||||||||||||||||||||||
| FPR = 0.28 | FPR = 0.77 | FPR = 0.88 | FPR = 0.12 | ||||||||||||||||||||||||||||||||||||
| PPV = 0.69 | PPV = 0.50 | PPV = 0.21 | PPV = 0.86 | ||||||||||||||||||||||||||||||||||||
| F1 = 0.66 | F1 = 0.61 | F1 = 0.22 | F1 = 0.81 | ||||||||||||||||||||||||||||||||||||
| ACC = 0.68 | ACC = 0.50 | ACC = 0.18 | ACC = 0.82 |
Plots of the four results above in the ROC space are given in the figure. The result of method A clearly shows the best predictive power among A, B, and C. The result of B lies on the random guess line (the diagonal line), and it can be seen in the table that the accuracy of B is 50%. However, when C is mirrored across the center point (0.5,0.5), the resulting method C′ is even better than A. This mirrored method simply reverses the predictions of whatever method or test produced the C contingency table. Although the original C method has negative predictive power, simply reversing its decisions leads to a new predictive method C′ which has positive predictive power. When the C method predicts p or n, the C′ method would predict n or p, respectively. In this manner, the C′ test would perform the best. The closer a result from a contingency table is to the upper left corner, the better it predicts, but the distance from the random guess line in either direction is the best indicator of how much predictive power a method has. If the result is below the line (i.e. the method is worse than a random guess), all of the method's predictions must be reversed in order to utilize its power, thereby moving the result above the random guess line.
Curves in ROC space
Classifications are often based on a continuous random variable. Write the probability for belonging in the class as a function of a decision/threshold parameter as and the probability of not belonging to the class as . The false positive rate FPR is given by and the true positive rate is . The ROC curve plots parametrically TPR(T) versus FPR(T) with T as the varying parameter.
For example, imagine that the blood protein levels in diseased people and healthy people are normally distributed with means of 2 g/dL and 1 g/dL respectively. A medical test might measure the level of a certain protein in a blood sample and classify any number above a certain threshold as indicating disease. The experimenter can adjust the threshold (black vertical line in the figure), which will in turn change the false positive rate. Increasing the threshold would result in fewer false positives (and more false negatives), corresponding to a leftward movement on the curve. The actual shape of the curve is determined by how much overlap the two distributions have.
Further interpretations
Sometimes, the ROC is used to generate a summary statistic. Common versions are:
- the intercept of the ROC curve with the line at 90 degrees to the no-discrimination line (also called Youden's J statistic)
- the area between the ROC curve and the no-discrimination line[citation needed]
- the area under the ROC curve, or "AUC" ("Area Under Curve"), or A' (pronounced "a-prime"),[2] or "c-statistic".[3]
- d' (pronounced "d-prime"), the distance between the mean of the distribution of activity in the system under noise-alone conditions and its distribution under signal-alone conditions, divided by their standard deviation, under the assumption that both these distributions are normal with the same standard deviation. Under these assumptions, it can be proved that the shape of the ROC depends only on d'.
However, any attempt to summarize the ROC curve into a single number loses information about the pattern of tradeoffs of the particular discriminator algorithm.
Area under the curve
When using normalized units, the area under the curve (often referred to as simply the AUC, or AUROC) is equal to the probability that a classifier will rank a randomly chosen positive instance higher than a randomly chosen negative one (assuming 'positive' ranks higher than 'negative').[4] This can be seen as follows: the area under the curve is given by (the integral boundaries are reversed as large T has a lower value on the x-axis)
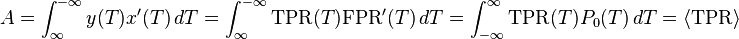 . The angular brackets denote average from the distribution of negative samples.
. The angular brackets denote average from the distribution of negative samples.
It can further be shown that the AUC is closely related to the Mann–Whitney U,[5][6] which tests whether positives are ranked higher than negatives. It is also equivalent to the Wilcoxon test of ranks.[6] The AUC is related to the Gini coefficient () by the formula , where:
- [7]
In this way, it is possible to calculate the AUC by using an average of a number of trapezoidal approximations.
It is also common to calculate the Area Under the ROC Convex Hull (ROC AUCH = ROCH AUC) as any point on the line segment between two prediction results can be achieved by randomly using one or other system with probabilities proportional to the relative length of the opposite component of the segment.[8] Interestingly, it is also possible to invert concavities – just as in the figure the worse solution can be reflected to become a better solution; concavities can be reflected in any line segment, but this more extreme form of fusion is much more likely to overfit the data.[9]
The machine learning community most often uses the ROC AUC statistic for model comparison.[10] However, this practice has recently been questioned based upon new machine learning research that shows that the AUC is quite noisy as a classification measure[11] and has some other significant problems in model comparison.[12][13] A reliable and valid AUC estimate can be interpreted as the probability that the classifier will assign a higher score to a randomly chosen positive example than to a randomly chosen negative example. However, the critical research[11][12] suggests frequent failures in obtaining reliable and valid AUC estimates. Thus, the practical value of the AUC measure has been called into question,[13] raising the possibility that the AUC may actually introduce more uncertainty into machine learning classification accuracy comparisons than resolution. Nonetheless, the coherence of AUC as a measure of aggregated classification performance has been vindicated, in terms of a uniform rate distribution,[14] and AUC has been linked to a number of other performance metrics such as the Brier score.[15]
One recent explanation of the problem with ROC AUC is that reducing the ROC Curve to a single number ignores the fact that it is about the tradeoffs between the different systems or performance points plotted and not the performance of an individual system, as well as ignoring the possibility of concavity repair, so that related alternative measures such as Informedness[16] or DeltaP are recommended.[17] These measures are essentially equivalent to the Gini for a single prediction point with DeltaP' = Informedness = 2AUC-1, whilst DeltaP = Markedness represents the dual (viz. predicting the prediction from the real class) and their geometric mean is the Matthews correlation coefficient.[16]
Other measures
In engineering, the area between the ROC curve and the no-discrimination line is sometimes preferred (equivalent to subtracting 0.5 from the AUC), and referred to as the discrimination'.[citation needed] In psychophysics, the sensitivity index d (d-prime), ΔP' or DeltaP' is the most commonly used measure[18] and is equivalent to twice the discrimination, being equal also to Informedness, deskewed WRAcc and Gini Coefficient in the single point case (single parameterization or single system).[16] These measures all have the advantage that 0 represents chance performance whilst 1 represents perfect performance, and -1 represents the "perverse" case of full informedness used to always give the wrong response.[19]
These varying choices of scale are fairly arbitrary since chance performance always has a fixed value: for AUC it is 0.5, but these alternative scales bring chance performance to 0 and allow them to be interpreted as Kappa statistics. Informedness has been shown to have desirable characteristics for Machine Learning versus other common definitions of Kappa such as Cohen Kappa and Fleiss Kappa.[16][20]
Sometimes it can be more useful to look at a specific region of the ROC Curve rather than at the whole curve. It is possible to compute partial AUC.[21] For example, one could focus on the region of the curve with low false positive rate, which is often of prime interest for population screening tests.[22] Another common approach for classification problems in which P ≪ N (common in bioinformatics applications) is to use a logarithmic scale for the x-axis.[23]
Detection error tradeoff graph
An alternative to the ROC curve is the detection error tradeoff (DET) graph, which plots the false negative rate (missed detections) vs. the false positive rate (false alarms) on non-linearly transformed x- and y-axes. The transformation function is the quantile function of the normal distribution, i.e., the inverse of the cumulative normal distribution. It is, in fact, the same transformation as zROC, below, except that the complement of the hit rate, the miss rate or false negative rate, is used. This alternative spends more graph area on the region of interest. Most of the ROC area is of little interest; one primarily cares about the region tight against the y-axis and the top left corner – which, because of using miss rate instead of its complement, the hit rate, is the lower left corner in a DET plot. The DET plot is used extensively in the automatic speaker recognition community, where the name DET was first used. The analysis of the ROC performance in graphs with this warping of the axes was used by psychologists in perception studies halfway the 20th century, where this was dubbed "double probability paper".[citation needed]
Z-score
If a standard score is applied to the ROC curve, the curve will be transformed into a straight line.[24] This z-score is based on a normal distribution with a mean of zero and a standard deviation of one. In memory strength theory, one must assume that the zROC is not only linear, but has a slope of 1.0. The normal distributions of targets (studied objects that the subjects need to recall) and lures (non studied objects that the subjects attempt to recall) is the factor causing the zROC to be linear.
The linearity of the zROC curve depends on the standard deviations of the target and lure strength distributions. If the standard deviations are equal, the slope will be 1.0. If the standard deviation of the target strength distribution is larger than the standard deviation of the lure strength distribution, then the slope will be smaller than 1.0. In most studies, it has been found that the zROC curve slopes constantly fall below 1, usually between 0.5 and 0.9.[25] Many experiments yielded a zROC slope of 0.8. A slope of 0.8 implies that the variability of the target strength distribution is 25% larger than the variability of the lure strength distribution.[26]
Another variable used is d' (d prime) (discussed above in "Other measures"), which can easily be expressed in terms of z-values. Although d' is a commonly used parameter, it must be recognized that it is only relevant when strictly adhering to the very strong assumptions of strength theory made above.[27]
The z-score of an ROC curve is always linear, as assumed, except in special situations. The Yonelinas familiarity-recollection model is a two-dimensional account of recognition memory. Instead of the subject simply answering yes or no to a specific input, the subject gives the input a feeling of familiarity, which operates like the original ROC curve. What changes, though, is a parameter for Recollection (R). Recollection is assumed to be all-or-none, and it trumps familiarity. If there were no recollection component, zROC would have a predicted slope of 1. However, when adding the recollection component, the zROC curve will be concave up, with a decreased slope. This difference in shape and slope result from an added element of variability due to some items being recollected. Patients with anterograde amnesia are unable to recollect, so their Yonelinas zROC curve would have a slope close to 1.0.[28]
History
The ROC curve was first used during World War II for the analysis of radar signals before it was employed in signal detection theory.[29] Following the attack on Pearl Harbor in 1941, the United States army began new research to increase the prediction of correctly detected Japanese aircraft from their radar signals.[citation needed]
In the 1950s, ROC curves were employed in psychophysics to assess human (and occasionally non-human animal) detection of weak signals.[29] In medicine, ROC analysis has been extensively used in the evaluation of diagnostic tests.[30][31] ROC curves are also used extensively in epidemiology and medical research and are frequently mentioned in conjunction with evidence-based medicine. In radiology, ROC analysis is a common technique to evaluate new radiology techniques.[32] In the social sciences, ROC analysis is often called the ROC Accuracy Ratio, a common technique for judging the accuracy of default probability models. ROC curves are widely used in laboratory medicine to assess diagnostic accuracy of a test, to choose the most optimal cut-off of a test and to compare diagnostic accuracy of several tests.
ROC curves also proved useful for the evaluation of machine learning techniques. The first application of ROC in machine learning was by Spackman who demonstrated the value of ROC curves in comparing and evaluating different classification algorithms.[33]
ROC curves beyond binary classification
The extension of ROC curves for classification problems with more than two classes has always been cumbersome, as the degrees of freedom increase quadratically with the number of classes, and the ROC space has dimensions, where is the number of classes.[34] Some approaches have been made for the particular case with three classes (three-way ROC).[35] The calculation of the volume under the ROC surface (VUS) has been analyzed and studied as a performance metric for multi-class problems.[36] However, because of the complexity of approximating the true VUS, some other approaches [37] based on an extension of AUC are more popular as an evaluation metric.
Given the success of ROC curves for the assessment of classification models, the extension of ROC curves for other supervised tasks has also been investigated. Notable proposals for regression problems are the so-called regression error characteristic (REC) Curves [38] and the Regression ROC (RROC) curves.[39] In the latter, RROC curves become extremely similar to ROC curves for classification, with the notions of asymmetry, dominance and convex hull. Also, the area under RROC curves is proportional to the error variance of the regression model.
ROC curve is related to the lift and uplift curves,[40][41] which are used in uplift modelling. The ROC curve itself has also been used as the optimization metric in uplift modeling.[42][43]
See also
| Statistics portal |
| Wikimedia Commons has media related to Receiver operating characteristic. |
Sources: Fawcett (2006) and Powers (2011).[44][45] |
- F1 score
- Brier score
- Coefficient of determination
- Constant false alarm rate
- Detection theory
- False alarm
- Gain (information retrieval)
- Precision and recall
- ROCCET
References
- ^ Swets, John A.; Signal detection theory and ROC analysis in psychology and diagnostics : collected papers, Lawrence Erlbaum Associates, Mahwah, NJ, 1996
- ^ Fogarty, James; Baker, Ryan S.; Hudson, Scott E. (2005). "Case studies in the use of ROC curve analysis for sensor-based estimates in human computer interaction". ACM International Conference Proceeding Series, Proceedings of Graphics Interface 2005. Waterloo, ON: Canadian Human-Computer Communications Society.
- ^ Hastie, Trevor; Tibshirani, Robert; Friedman, Jerome H. (2009). The elements of statistical learning: data mining, inference, and prediction (2nd ed.).
- ^ Fawcett, Tom (2006); An introduction to ROC analysis, Pattern Recognition Letters, 27, 861–874.
- ^ Hanley, James A.; McNeil, Barbara J. (1982). "The Meaning and Use of the Area under a Receiver Operating Characteristic (ROC) Curve". Radiology 143 (1): 29–36. doi:10.1148/radiology.143.1.7063747. PMID 7063747.
- ^ a b Mason, Simon J.; Graham, Nicholas E. (2002). "Areas beneath the relative operating characteristics (ROC) and relative operating levels (ROL) curves: Statistical significance and interpretation" (PDF). Quarterly Journal of the Royal Meteorological Society 128: 2145–2166. doi:10.1256/003590002320603584.
- ^ Hand, David J.; and Till, Robert J. (2001); A simple generalization of the area under the ROC curve for multiple class classification problems, Machine Learning, 45, 171–186.
- ^ Provost, F.; Fawcett, T. (2001). "Robust classification for imprecise environments.". Machine Learning, 44: 203–231.
- ^ Flach, P.A.; Wu, S. (2005). "Repairing concavities in ROC curves." (PDF). 19th International Joint Conference on Artificial Intelligence (IJCAI'05). pp. 702–707.
- ^ Hanley, James A.; McNeil, Barbara J. (1983-09-01). "A method of comparing the areas under receiver operating characteristic curves derived from the same cases". Radiology 148 (3): 839–843. doi:10.1148/radiology.148.3.6878708. PMID 6878708. Retrieved 2008-12-03.
- ^ a b Hanczar, Blaise; Hua, Jianping; Sima, Chao; Weinstein, John; Bittner, Michael; and Dougherty, Edward R. (2010); Small-sample precision of ROC-related estimates, Bioinformatics 26 (6): 822–830
- ^ a b Lobo, Jorge M.; Jiménez-Valverde, Alberto; and Real, Raimundo (2008), AUC: a misleading measure of the performance of predictive distribution models, Global Ecology and Biogeography, 17: 145–151
- ^ a b Hand, David J. (2009); Measuring classifier performance: A coherent alternative to the area under the ROC curve, Machine Learning, 77: 103–123
- ^ Flach, P.A.; Hernandez-Orallo, J.; Ferri, C. (2011). "A coherent interpretation of AUC as a measure of aggregated classification performance." (PDF). Proceedings of the 28th International Conference on Machine Learning (ICML-11). pp. 657–664.
- ^ Hernandez-Orallo, J.; Flach, P.A.; Ferri, C. (2012). "A unified view of performance metrics: translating threshold choice into expected classification loss" (PDF). Journal of Machine Learning Research 13: 2813–2869.
- ^ a b c d Powers, David M W (2011) [2007]. "Evaluation: From Precision, Recall and F-Measure to ROC, Informedness, Markedness & Correlation" (PDF). Journal of Machine Learning Technologies 2 (1): 37–63. [1]
- ^ Powers, David M.W. (2012). "The Problem of Area Under the Curve". International Conference on Information Science and Technology.
- ^ Perruchet, P.; Peereman, R. (2004). "The exploitation of distributional information in syllable processing". J. Neurolinguistics 17: 97–119. doi:10.1016/s0911-6044(03)00059-9.
- ^ Powers, David M. W. (2003). "Recall and Precision versus the Bookmaker" (PDF). Proceedings of the International Conference on Cognitive Science (ICSC- 2003), Sydney Australia, 2003, pp.529-534.
- ^ Powers, David M. W. (2012). "The Problem with Kappa" (PDF). Conference of the European Chapter of the Association for Computational Linguistics (EACL2012) Joint ROBUS-UNSUP Workshop.
- ^ McClish, Donna Katzman (1989-08-01). "Analyzing a Portion of the ROC Curve". Medical Decision Making 9 (3): 190–195. doi:10.1177/0272989X8900900307. PMID 2668680. Retrieved 2008-09-29.
- ^ Dodd, Lori E.; Pepe, Margaret S. (2003). "Partial AUC Estimation and Regression". Biometrics 59 (3): 614–623. doi:10.1111/1541-0420.00071. PMID 14601762. Retrieved 2007-12-18.
- ^ Karplus, Kevin (2011); Better than Chance: the importance of null models, University of California, Santa Cruz, in Proceedings of the First International Workshop on Pattern Recognition in Proteomics, Structural Biology and Bioinformatics (PR PS BB 2011)
- ^ MacMillan, Neil A.; Creelman, C. Douglas (2005). Detection Theory: A User's Guide (2nd ed.). Mahwah, NJ: Lawrence Erlbaum Associates. ISBN 1-4106-1114-0.
- ^ Glanzer, Murray; Kisok, Kim; Hilford, Andy; Adams, John K. (1999). "Slope of the receiver-operating characteristic in recognition memory". Journal of Experimental Psychology: Learning, Memory, and Cognition 25 (2): 500–513. doi:10.1037/0278-7393.25.2.500.
- ^ Ratcliff, Roger; McCoon, Gail; Tindall, Michael (1994). "Empirical generality of data from recognition memory ROC functions and implications for GMMs". Journal of Experimental Psychology: Learning, Memory, and Cognition 20: 763–785. doi:10.1037/0278-7393.20.4.763.
- ^ Zhang, Jun; Mueller, Shane T. (2005). "A note on ROC analysis and non-parametric estimate of sensitivity". Psychometrika 70 (203-212).
- ^ Yonelinas, Andrew P.; Kroll, Neal E. A.; Dobbins, Ian G.; Lazzara, Michele; Knight, Robert T. (1998). "Recollection and familiarity deficits in amnesia: Convergence of remember-know, process dissociation, and receiver operating characteristic data". Neuropsychology 12: 323–339. doi:10.1037/0894-4105.12.3.323.
- ^ a b Green, David M.; Swets, John A. (1966). Signal detection theory and psychophysics. New York, NY: John Wiley and Sons Inc. ISBN 0-471-32420-5.
- ^ Zweig, Mark H.; Campbell, Gregory (1993). "Receiver-operating characteristic (ROC) plots: a fundamental evaluation tool in clinical medicine" (PDF). Clinical Chemistry 39 (8): 561–577. PMID 8472349.
- ^ Pepe, Margaret S. (2003). The statistical evaluation of medical tests for classification and prediction. New York, NY: Oxford. ISBN 0-19-856582-8.
- ^ Obuchowski, Nancy A. (2003). "Receiver operating characteristic curves and their use in radiology". Radiology 229 (1): 3–8. doi:10.1148/radiol.2291010898. PMID 14519861.
- ^ Spackman, Kent A. (1989). "Signal detection theory: Valuable tools for evaluating inductive learning". Proceedings of the Sixth International Workshop on Machine Learning. San Mateo, CA: Morgan Kaufmann. pp. 160–163.
- ^ Srinivasan, A. (1999). "Note on the Location of Optimal Classifiers in N-dimensional ROC Space". Technical Report PRG-TR-2-99, Oxford University Computing Laboratory, Wolfson Building, Parks Road, Oxford.
- ^ Mossman, D. (1999). "Three-way ROCs". Medical Decision Making 19: 78–89. doi:10.1177/0272989x9901900110.
- ^ Ferri, C.; Hernandez-Orallo, J.; Salido, M.A. (2003). "Volume under the ROC Surface for Multi-class Problems". Machine Learning: ECML 2003. pp. 108–120.
- ^ Till, D.J.; Hand, R.J. (2012). "A Simple Generalisation of the Area Under the ROC Curve for Multiple Class Classification Problems". Machine Learning 45: 171–186. doi:10.1023/A:1010920819831.
- ^ Bi, J.; Bennett, K.P. (2003). "Regression error characteristic curves". Twentieth International Conference on Machine Learning (ICML-2003). Washington, DC.
- ^ Hernandez-Orallo, J. (2013). "ROC curves for regression". Pattern Recognition 46 (12): 3395–3411 . doi:10.1016/j.patcog.2013.06.014.
- ^ Tufféry, Stéphane (2011); Data Mining and Statistics for Decision Making, Chichester, GB: John Wiley & Sons, translated from the French Data Mining et statistique décisionnelle (Éditions Technip, 2008)
- ^ Kuusisto, Finn; Santos Costa, Vitor; nassif, Houssam; Burnside, Elizabeth; Page, David; Shavlik, Jude (2014). "Support Vector Machines for Differential Prediction" (PDF). European Conference on Machine Learning (ECML'14) (Nancy, France): 50–65.
- ^ Nassif, Houssam; Kuusisto, Finn; Burnside, Elizabeth; Shavlik, Jude (2013). "Uplift Modeling with ROC: An SRL Case Study" (PDF). International Conference on Inductive Logic Programming (Rio de Janeiro, Brazil): 40–45 Late Breaking Papers.
- ^ Nassif, Houssam; Wu, Yirong; Page, David; Burnside, Elizabeth (2012). "Logical Differential Prediction Bayes Net, Improving Breast Cancer Diagnosis for Older Women" (PDF). American Medical Informatics Association Symposium (AMIA'12) (Chicago): 1330–1339. Retrieved 18 July 2014.
- ^ Fawcett, Tom (2006). "An Introduction to ROC Analysis". Pattern Recognition Letters 27 (8): 861 – 874. doi:10.1016/j.patrec.2005.10.010.
- ^ Powers, David M W (2011). "Evaluation: From Precision, Recall and F-Measure to ROC, Informedness, Markedness & Correlation" (PDF). Journal of Machine Learning Technologies 2 (1): 37–63.
General references
- Zhou, Xiao-Hua; Obuchowski, Nancy A.; McClish, Donna K. (2002). Statistical Methods in Diagnostic Medicine. New York, NY: Wiley & Sons. ISBN 978-0-471-34772-9.
Further reading
- Balakrishnan, Narayanaswamy (1991); Handbook of the Logistic Distribution, Marcel Dekker, Inc., ISBN 978-0-8247-8587-1
- Brown, Christopher D.; and Davis, Herbert T. (2006); Receiver operating characteristic curves and related decision measures: a tutorial, Chemometrics and Intelligent Laboratory Systems, 80:24–38
- Fawcett, Tom (2004); ROC Graphs: Notes and Practical Considerations for Researchers, Pattern Recognition Letters, 27(8):882–891.
- Gonen, Mithat (2007); Analyzing Receiver Operating Characteristic Curves Using SAS, SAS Press, ISBN 978-1-59994-298-8
- Green, William H., (2003) Econometric Analysis, fifth edition, Prentice Hall, ISBN 0-13-066189-9
- Heagerty, Patrick J.; Lumley, Thomas; and Pepe, Margaret S. (2000); Time-dependent ROC Curves for Censored Survival Data and a Diagnostic Marker, Biometrics, 56:337–344
- Hosmer, David W.; and Lemeshow, Stanley (2000); Applied Logistic Regression, 2nd ed., New York, NY: Wiley, ISBN 0-471-35632-8
- Lasko, Thomas A.; Bhagwat, Jui G.; Zou, Kelly H.; and Ohno-Machado, Lucila (2005); The use of receiver operating characteristic curves in biomedical informatics, Journal of Biomedical Informatics, 38(5):404–415
- Stephan, Carsten; Wesseling, Sebastian; Schink, Tania; and Jung, Klaus (2003); Comparison of Eight Computer Programs for Receiver-Operating Characteristic Analysis, Clinical Chemistry, 49:433–439
- Swets, John A.; Dawes, Robyn M.; and Monahan, John (2000); Better Decisions through Science, Scientific American, October, pp. 82–87
- Zou, Kelly H.; O'Malley, A. James; Mauri, Laura (2007); Receiver-operating characteristic analysis for evaluating diagnostic tests and predictive models, Circulation, 115(5):654–7
External links
- ROC curves. Biomedical statistics
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
UpToDate Contents
全文を閲覧するには購読必要です。 To read the full text you will need to subscribe.
- 1. 診断的検査の評価 evaluating diagnostic tests
- 2. 生物統計学および疫学に関する一般用語集 glossary of common biostatistical and epidemiological terms
- 3. 前立腺癌のスクリーニング screening for prostate cancer
- 4. 乳癌スクリーニングのためのリスク予測 risk prediction for breast cancer screening
- 5. 遺伝関連研究:原理および応用 genetic association studies principles and applications
English Journal
- Diagnostic accuracy of quantitative neuromuscular ultrasound for the diagnosis of intensive care unit-acquired weakness: a cross-sectional observational study.
- Witteveen E1,2,3, Sommers J4, Wieske L5,6,7, Doorduin J8,9, van Alfen N8, Schultz MJ5,6, van Schaik IN7, Horn J5,6, Verhamme C7.
- Annals of intensive care.Ann Intensive Care.2017 Dec;7(1):40. doi: 10.1186/s13613-017-0263-8. Epub 2017 Apr 5.
- PMID 28382599
- Performance of risk assessment tools for predicting osteoporosis in south Indian rural elderly men.
- Satyaraddi A1, Shetty S1, Kapoor N1, Cherian KE1, Naik D1, Thomas N1, Paul TV2.
- Archives of osteoporosis.Arch Osteoporos.2017 Dec;12(1):35. doi: 10.1007/s11657-017-0332-5. Epub 2017 Apr 5.
- PMID 28378274
- Evaluation of the validity of osteoporosis and fracture risk assessment tools (IOF One Minute Test, SCORE, and FRAX) in postmenopausal Palestinian women.
- Kharroubi A1, Saba E2, Ghannam I3, Darwish H2,4,5.
- Archives of osteoporosis.Arch Osteoporos.2017 Dec;12(1):6. doi: 10.1007/s11657-016-0298-8. Epub 2016 Dec 24.
- PMID 28013446
Japanese Journal
- Diagnostic Accuracy of Recombinant Immunoglobulin-like Protein A-Based IgM ELISA for the Early Diagnosis of Leptospirosis in the Philippines
- PLOS Neglected Tropical Diseases 9(6), e0003879, 2015-06-25
- NAID 120005624095
- 急性期病院の内科疾患入院患者における自立歩行の関連因子とカットオフ値の検討
- 理学療法学 42(3), 237-245, 2015-06-20
- NAID 110009970964
- Asymptotic Properties of Area Under the ROC Curve via Likelihood Ratio Based Ranking Function (情報論的学習理論と機械学習)
- 電子情報通信学会技術研究報告 = IEICE technical report : 信学技報 114(502), 55-62, 2015-03-05
- NAID 40020432211
Related Links
- Clinical Journal Club 5. ROC曲線 ROC曲線(Receiver Operatorating Characteristic curve、受信者動作特性曲線)は、もともとレーダーシステムの通信工学理論として開発されたものであり、レーダー信号のノイズの中から敵機の存在を検出 ...
- ROC曲線下の面積(Area under the curve,AUC)は分類器(分類のアルゴリズム)の性能の良さを表します。0から1までの値をとり,完全な分類が可能なときの面積は1で,ランダムな分類の場合は0.5になります。 AUCの値は,TとF ...
Related Pictures
★リンクテーブル★
| リンク元 | 「ROC曲線」「受信者動作特性曲線」「受診者動作特性曲線」「receiver operating characteristic」「receiver operating characteristic curve」 |
| 関連記事 | 「R」「curve」 |
「ROC曲線」
- 英
- receiver operating characteristic curve, ROC curve
- 同
- 受診者動作特性曲線、受診者操作特性曲線、受信者動作特性曲線
- 検査の偽陽性割合と感度のプロットから健常人と患者の識別点を評価する方法
- カットオフ値(カットオフポイント)はROC曲線の左上に近い点を採用する(感度、特異度最大の所)
「受信者動作特性曲線」
「受診者動作特性曲線」
「receiver operating characteristic」
「receiver operating characteristic curve」
「R」
「curve」
- n.
- v.
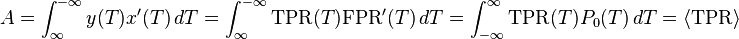 . The angular brackets denote average from the distribution of negative samples.
. The angular brackets denote average from the distribution of negative samples.